题目内容
已知等差数列{an}的前n项之和是Sn,则-am<a1<-am+1是Sm>0,Sm+1<0的( )A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
【答案】分析:根据等差数列的前n项和公式Sn=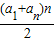 ,观察当-am<a1<-am+1时,先得出am+a1>0,a1+am+1<0,从而Sm>0,Sm+1<0;反之,当Sm>0,Sm+1<0时,得am+a1>0,a1+am+1<0,也有-am<a1<-am+1成立.从而得出答案.
,观察当-am<a1<-am+1时,先得出am+a1>0,a1+am+1<0,从而Sm>0,Sm+1<0;反之,当Sm>0,Sm+1<0时,得am+a1>0,a1+am+1<0,也有-am<a1<-am+1成立.从而得出答案.
解答:解:根据等差数列的前n项和公式Sn=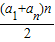 ,得,
,得,
当-am<a1<-am+1时,得am+a1>0,a1+am+1<0,从而Sm>0,Sm+1<0;
反之,当Sm>0,Sm+1<0时,得am+a1>0,a1+am+1<0,∴-am<a1<-am+1.
则-am<a1<-am+1是Sm>0,Sm+1<0的充分必要条件.
故选C.
点评:本题主要考查了等差数列的前n项和公式、必要条件、充分条件与充要条件的判断.属于基础题.
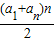 ,观察当-am<a1<-am+1时,先得出am+a1>0,a1+am+1<0,从而Sm>0,Sm+1<0;反之,当Sm>0,Sm+1<0时,得am+a1>0,a1+am+1<0,也有-am<a1<-am+1成立.从而得出答案.
,观察当-am<a1<-am+1时,先得出am+a1>0,a1+am+1<0,从而Sm>0,Sm+1<0;反之,当Sm>0,Sm+1<0时,得am+a1>0,a1+am+1<0,也有-am<a1<-am+1成立.从而得出答案.解答:解:根据等差数列的前n项和公式Sn=
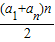 ,得,
,得,当-am<a1<-am+1时,得am+a1>0,a1+am+1<0,从而Sm>0,Sm+1<0;
反之,当Sm>0,Sm+1<0时,得am+a1>0,a1+am+1<0,∴-am<a1<-am+1.
则-am<a1<-am+1是Sm>0,Sm+1<0的充分必要条件.
故选C.
点评:本题主要考查了等差数列的前n项和公式、必要条件、充分条件与充要条件的判断.属于基础题.

练习册系列答案
相关题目
 已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.
已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.