题目内容
6.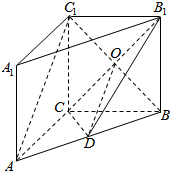 如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,AC⊥BC,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,AC⊥BC,点D是AB的中点.(1)求证:CD⊥平面ABB1A1
(2)求证:AC1∥平面CDB1
(3)求三棱锥B-CDB1的体积.
分析 (1)由AC=BC=2,点D是AB的中点,可得CD⊥AB.由直三棱柱ABC-A1B1C1中,可得AA1⊥CD,即可证明;
(2)点O为矩形CBB1C1的对角线交点,可得:C1O=OB,利用三角形中位线定理可得:AC1∥OD,利用线面平行的判定定理可得:AC1∥平面CDB1.
(3)由AC=BC=2,AC⊥BC,点D是AB的中点.可得S△CDB=$\frac{1}{2}×\frac{1}{2}×AC×BC$.利用三棱锥B-CDB1的体积V=$\frac{1}{3}×{S}_{△CDB}$×B1B即可得出.
解答 (1)证明:∵AC=BC=2,点D是AB的中点.∴CD⊥AB.
由直三棱柱ABC-A1B1C1中,∴AA1⊥底面ABC,∴AA1⊥CD,
又AB∩AA1=A,∴CD⊥平面平面ABB1A1.
(2)证明:∵点O为矩形CBB1C1的对角线交点,
∴C1O=OB,
又AD=DB,
∴AC1∥OD,
又AC1?平面CDB1,OD?平面CDB1.
∴AC1∥平面CDB1.
(3)解:∵AC=BC=2,AC⊥BC,点D是AB的中点.
∴S△CDB=$\frac{1}{2}×\frac{1}{2}×AC×BC$=1.
∴三棱锥B-CDB1的体积V=$\frac{1}{3}×{S}_{△CDB}$×B1B
=$\frac{1}{3}×1×2$
=$\frac{2}{3}$.
点评 本题考查了空间线面位置关系、三棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
11.某几何体的三视图如图所示,则该几何体的体积等于( )
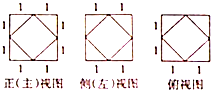

| A. | $\frac{26}{3}$ | B. | $\frac{25}{3}$ | C. | $\frac{22}{3}$ | D. | $\frac{20}{3}$ |
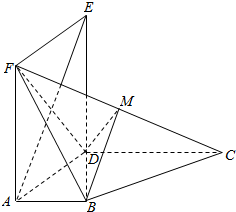 如图所示,平面ADEF⊥平面ABCD,且四边形ADEF为正方形,AD⊥DC,AB∥CD,AB=AD=$\frac{1}{2}$DC=2,M为CE的中点.
如图所示,平面ADEF⊥平面ABCD,且四边形ADEF为正方形,AD⊥DC,AB∥CD,AB=AD=$\frac{1}{2}$DC=2,M为CE的中点.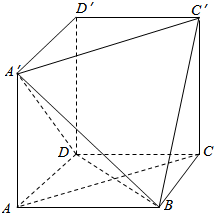 在长方体ABCD-A′B′C′D′中,AB=BC=2,过A′,C′,B三点的平面截去长方体的一个角后,得到ABCD-A′C′D′,
在长方体ABCD-A′B′C′D′中,AB=BC=2,过A′,C′,B三点的平面截去长方体的一个角后,得到ABCD-A′C′D′,