题目内容
若实数x,y满足不等式组 则
则 的最大值为
的最大值为
- A.
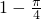
- B.

- C.

- D.
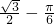
D
分析:本题主要考查线性规划的基本知识,先画出约束条件 可行域,再求出可行域中切线的斜率为
可行域,再求出可行域中切线的斜率为 点的坐标,分析后易得目标函数
点的坐标,分析后易得目标函数 的最大值.
的最大值.
解答: 解:如图,阴影部分为满足条件的点(x,y)的集合对应的平面区域,
解:如图,阴影部分为满足条件的点(x,y)的集合对应的平面区域,
∵(sinx)′=cosx,
y= x+z,
x+z,
∴cosx0= ,∴x0=
,∴x0=
∴点( ,
, )为目标函数即得最大值的最优解,
)为目标函数即得最大值的最优解,
即z的最小值为: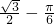 .
.
点评:线性规划问题首先作出可行域,若为封闭区域(即几条图象围成的区域)则区域边界的值是目标函数取得最大或最小值,求出直线交点坐标代入目标函数即可求出最大值.
分析:本题主要考查线性规划的基本知识,先画出约束条件
 可行域,再求出可行域中切线的斜率为
可行域,再求出可行域中切线的斜率为 点的坐标,分析后易得目标函数
点的坐标,分析后易得目标函数 的最大值.
的最大值.解答:
 解:如图,阴影部分为满足条件的点(x,y)的集合对应的平面区域,
解:如图,阴影部分为满足条件的点(x,y)的集合对应的平面区域,∵(sinx)′=cosx,
y=
 x+z,
x+z,∴cosx0=
 ,∴x0=
,∴x0=
∴点(
 ,
, )为目标函数即得最大值的最优解,
)为目标函数即得最大值的最优解,即z的最小值为:
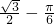 .
.点评:线性规划问题首先作出可行域,若为封闭区域(即几条图象围成的区域)则区域边界的值是目标函数取得最大或最小值,求出直线交点坐标代入目标函数即可求出最大值.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 ,且对于任意的x,y∈R,不等式f(x2-2x)+f(2y-y2)≤0成立.又函数y=f(x-1)的图象关于点(1,0)对称,则当 1≤x≤4时,
,且对于任意的x,y∈R,不等式f(x2-2x)+f(2y-y2)≤0成立.又函数y=f(x-1)的图象关于点(1,0)对称,则当 1≤x≤4时, 的取值范围为 .
的取值范围为 . ,且对于任意的x,y∈R,不等式f(x2-2x)+f(2y-y2)≤0成立.又函数y=f(x-1)的图象关于点(1,0)对称,则当 1≤x≤4时,
,且对于任意的x,y∈R,不等式f(x2-2x)+f(2y-y2)≤0成立.又函数y=f(x-1)的图象关于点(1,0)对称,则当 1≤x≤4时, 的取值范围为 .
的取值范围为 . ,且对于任意的x,y∈R,不等式f(x2-2x)+f(2y-y2)≤0成立.又函数y=f(x-1)的图象关于点(1,0)对称,则当 1≤x≤4时,
,且对于任意的x,y∈R,不等式f(x2-2x)+f(2y-y2)≤0成立.又函数y=f(x-1)的图象关于点(1,0)对称,则当 1≤x≤4时, 的取值范围为 .
的取值范围为 . ,且对于任意的x,y∈R,不等式f(x2-2x)+f(2y-y2)≤0成立.又函数y=f(x-1)的图象关于点(1,0)对称,则当 1≤x≤4时,
,且对于任意的x,y∈R,不等式f(x2-2x)+f(2y-y2)≤0成立.又函数y=f(x-1)的图象关于点(1,0)对称,则当 1≤x≤4时, 的取值范围为 .
的取值范围为 .