题目内容

等比数列{a_n}中，a₁=cosx，x∈（0，π），公比q=sinx，若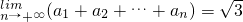 $数学公式$ ，则x=________．

$\text{[math]}$
分析：由数列{a_n}为等比数列可知，sinx≠1时，由x∈（0，π）可得sinx∈（0，1）．利用等比数列的前 n项和公式先求
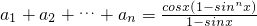$\text{[math]}$ 代入极限运算可得 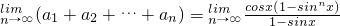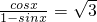$\text{[math]}$ = $\text{[math]}$ 从而可得 $\text{[math]}$ 利用辅助角公式可得sin（x+ $\text{[math]}$ ）= $\text{[math]}$ 结合x∈（0，π）且sinx≠1可求x
解答：因为数列{a_n}为等比数列
当sinx=1，cosx=0不符合等比数列的条件，故舍去
当sinx≠1时，由x∈（0，π）可得sinx∈（0，1）
由等比数列的前 n项和公式可得，
$\text{[math]}$
∴ $\text{[math]}$ = $\text{[math]}$
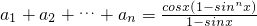
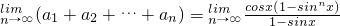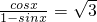
∴ $\text{[math]}$ 即 sin（x+ $\text{[math]}$ ）= $\text{[math]}$
∵x∈（0，π）且sinx≠1∴x= $\text{[math]}$
故答案为： $\text{[math]}$
点评：本题主要考查了等比数列的定义及前 n项和公式的运用，还考查了极限及运算，三角函数的辅助角公式的运用，属于基础知识的简单综合．