题目内容

l1、l2是异面直线,A、B∈l1,A1、B1∈l2,AA1⊥l2,BB1⊥l2.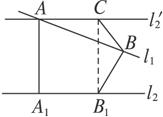

(1)当A1、B1重合时,求证:l1⊥l2;

(2)当l1、l2所成的角为θ(0＜θ＜)并且AB=a时,求A1B1的长.

(1)证明:当A1、B1重合时,设重合后的点为P,则PA⊥l2,PB⊥l2,∴l2⊥平面PAB,AB平面PAB.∴l2⊥AB,即l1⊥l2.

(2)解析:过A作l2′∥l2,在l2′上取点C,使AC=A1B1,则∠CBA=θ,且AA1B1C是平行四边形,∴B1C∥AA1.由AA1⊥l2得l2⊥B1C.由BB1⊥l2得l2⊥平面B1BC.

∵l2′∥l2,

∴l2′⊥平面B1BC.

∴∠ACB=90°.在△ACB中,AB=a,∠CAB=θ,

∴AC=ABcosθ=acosθ,即A1B1=acosθ.

练习册系列答案
相关题目
6、在平面上，两条直线的位置关系有相交、平行、重合三种．已知α，β是两个相交平面，空间两条直线l1，l2在α上的射影是直线S1，S2，l1，l2在β上的射影是直线t1，t2．用S1与S2，t1与t2的位置关系，写出一个总能确定l1与l2是异面直线的充分条件：
S1∥S2，并且t1与t2相交（或：t1∥t2，并且S1与S2相交）
．
4、给出下列四个命题：
①垂直于同一直线的两条直线互相平行．
②垂直于同一平面的两个平面互相平行．
③若直线l1，l2与同一平面所成的角相等，则l1，l2互相平行．
④若直线l1，l2是异面直线，则与l1，l2都相交的两条直线是异面直线．
其中假命题的个数是（　　）
10、平面内两直线有三种位置关系：相交，平行与重合．已知两个相交平面α，β与两直线l1，l2，又知l1，l2在α内的射影为s1，s2，在β内的射影为t1，t2．试写出s1，s2与t1，t2满足的条件，使之一定能成为l1，l2是异面直线的充分条件
s1∥s2，并且t1与t2相交（t1∥t2，并且s1与s2相交）
．
给出下列四个命题：①平行于母线的平面截圆锥，截面是等腰三角形；②圆柱是将矩形旋转一周所得的几何体；③若直线l1，l2与同一平面所成的角相等，则l1，l2互相平行；④若直线l1，l2是异面直线，则与l1，l2都相交的两条直线是异面直线，其中假命题的个数是（　　）
给出下列四个命题：
①垂直于同一直线的两条直线互相平行       
②垂直于同一平面的两个平面互相平行
③若直线l1，l2与同一平面所成的角相等，则l1，l2互相平行   
④若直线l1，l2是异面直线，则与l1，l2都相交的两条直线是异面直线．
其中假命题的个数是
4
4
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网