题目内容
已知正方形ABCD的中心在原点,四个顶点都在函数f(x)=ax3+bx(a>0)图象上.若正方形ABCD唯一确定,则b的值为________.
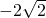
分析:设正方形ABCD对角线AC所在的直线方程为y=kx,则其斜率唯一确定,转化为二元方程只有唯一实数根,利用根的判别式求解即可.
解答:设正方形ABCD对角线AC所在的直线方程为y=kx(k≠0),
则对角线BD所在的直线方程为y=-
 x.
x.由
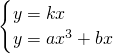 ,解得x2=
,解得x2=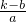 ,
,所以AO2=x2+y2=(1+k2)x2=(1+k2)•
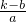 ,
,同理,BO2=[1+(-
 )2]•
)2]•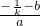 =
=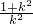 •
•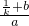 ,
,又因为AO2=BO2,所以k3-k2b+
 +b=0.
+b=0.即k2+
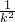 -b(k-
-b(k- )=0,即(k-
)=0,即(k- )2-b(k-
)2-b(k- )+2=0.
)+2=0.令k-
 =t得t2-bt+2=0
=t得t2-bt+2=0因为正方形ABCD唯一确定,则对角线AC与BD唯一确定,于是k-
 值唯一确定,
值唯一确定,所以关于t的方程t2-bt+2=0有且只有一个实数根,又k-
 =t∈R.
=t∈R.所以△=b2-8=0,即b=±2
 .
.因为x2=
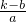 >0,a>0,所以b<k;又
>0,a>0,所以b<k;又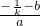 >0,所以b<-
>0,所以b<- ,故b<0.
,故b<0.因此b=-2
 ;
;反过来b=-2
 时,t=-
时,t=- ,k-
,k- =-
=- ,
,于是k=
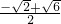 ,-
,- =
= ;或k=
;或k= ,-
,- =
=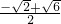 .
.于是正方形ABCD唯一确定.
故答案为:
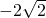 .
.点评:本小题主要考查函数的解析式的求法以及导数,单调性,不等式等基础知识,考查综合利用数学知识分析问题、解决问题的能力.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
已知正方形ABCD的边长为1,设
=
,
=
,
=
,则|
-
+
|等于( )
| AB |
| a |
| BC |
| b |
| AC |
| c |
| a |
| b |
| c |
| A、0 | ||
B、
| ||
| C、2 | ||
D、2
|
 已知正方形ABCD的边长为2,中心为O,四边形PACE是直角梯形,设PA⊥平面ABCD,且PA=2,CE=1,
已知正方形ABCD的边长为2,中心为O,四边形PACE是直角梯形,设PA⊥平面ABCD,且PA=2,CE=1, 如图,已知正方形ABCD的中心为E(-1,0),一边AB所在的直线方程为x+3y-5=0,求其它三边所在的直线方程.
如图,已知正方形ABCD的中心为E(-1,0),一边AB所在的直线方程为x+3y-5=0,求其它三边所在的直线方程.