题目内容
15.函数f(x)=$\left\{\begin{array}{l}{{4}^{x}(x≤\frac{1}{2})}\\{lo{g}_{a}x(x>\frac{1}{2})}\end{array}\right.$的最大值是2,则a的取值范围是0<a<$\frac{\sqrt{2}}{2}$..分析 对分段函数分区间求解:当x≤$\frac{1}{2}$时,f(x)=4x≤$\sqrt{4}$=2,当x>$\frac{1}{2}$时,
f(x)=logax<2,可得0<a<1,且loga$\frac{1}{2}$≤2,求解即可.
解答 解:当x≤$\frac{1}{2}$时,
f(x)=4x≤$\sqrt{4}$=2,
∵函数的最大值是2,
∴当x>$\frac{1}{2}$时,
f(x)=logax<2,
∴0<a<1,且loga$\frac{1}{2}$≤2,
∴0<a<$\frac{\sqrt{2}}{2}$.
故a的取值范围是0<a<$\frac{\sqrt{2}}{2}$.
点评 考查了分段函数,结合题意,得出函数满足的表达式.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
20.已知数列{an}满足a2=34,an+1-an=4n(n∈N*),则数列{$\frac{{a}_{n}}{n}$}的最小值是( )
| A. | 15 | B. | 14 | C. | $\frac{27}{2}$ | D. | 16 |
 如图,该程序框图的算法思路源于我国古代数学专著《九章算术》中的“更相减损术”,执行此程序框图,若输入的m,n分别为72,168,则输出的m=( )
如图,该程序框图的算法思路源于我国古代数学专著《九章算术》中的“更相减损术”,执行此程序框图,若输入的m,n分别为72,168,则输出的m=( )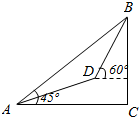 某登山队在山脚A处测得山顶B的仰角为45°,沿倾斜角为30°的斜坡前进1000m后到达D处,又测得山顶的仰角为60°,则山的高度BC为$500(\sqrt{3}+1)$m.
某登山队在山脚A处测得山顶B的仰角为45°,沿倾斜角为30°的斜坡前进1000m后到达D处,又测得山顶的仰角为60°,则山的高度BC为$500(\sqrt{3}+1)$m.