题目内容
在△ABC中,a,b,c分别为角A、B、C的对边,
4sin2 -cos2A=
-cos2A= .
.
(1)求A的度数;
(2)若a= ,b+c=3,求b与c的值.
,b+c=3,求b与c的值.
(1)由条件得2[1-cos(B+C)]-2cos2A+1= .
.
∴4(1+cosA)-4cos2A=5,∴(2cosA-1)2=0,
∴cosA=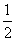 ,∵0°<A<180°,∴A=60°.
,∵0°<A<180°,∴A=60°.
(2)由余弦定理得, =
=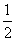 ,
,
化简并整理得(b+c)2-a2=3bc,
将a= ,b+c=3代入上式,得bc=2.
,b+c=3代入上式,得bc=2.
联立b+c=3与bc=2,解得b=1,c=2或b=2,c=1

练习册系列答案
相关题目
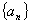 是等差数列,且
是等差数列,且 ,
,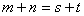 ;
;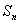 是等差数列
是等差数列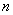 项的和,则
项的和,则 成等差数列;
成等差数列;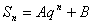 ;(其中
;(其中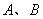 是非零常数,
是非零常数, ),则
),则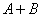 为零.
为零.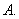 ①②
①② 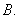 ②③
②③ 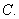 ②④
②④  ③④
③④ 的解集是
的解集是  .
.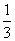 ,则底角的正弦值为________
,则底角的正弦值为________ ,91,92,…,99.现在从第
,91,92,…,99.现在从第 组中抽取其号码的个位数与
组中抽取其号码的个位数与 的个位数相同的个体,其中
的个位数相同的个体,其中 是第1组随机抽取的号码的个位数,则当
是第1组随机抽取的号码的个位数,则当 时,从第7组中抽取的号码是( )
时,从第7组中抽取的号码是( ) .
. B.
B. C.
C. D.
D.
 中,
中, ,则
,则
 B.
B. C.
C. D.
D.
 前
前 项之和是
项之和是 ,
, ,那么数列的通项公式是
,那么数列的通项公式是