题目内容
(本小题满分13分)已知数列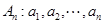 .如果数列
.如果数列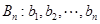 满足
满足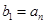 ,
,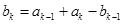 ,其中
,其中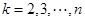 ,则称
,则称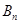 为
为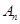 的“衍生数列”.
的“衍生数列”.
(Ⅰ)写出数列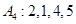 的“衍生数列”
的“衍生数列”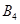 ;
;
(Ⅱ)若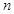 为偶数,且
为偶数,且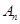 的“衍生数列”是
的“衍生数列”是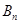 ,证明:
,证明: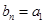 ;
;
(Ⅲ)若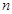 为奇数,且
为奇数,且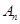 的“衍生数列”是
的“衍生数列”是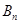 ,
,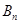 的“衍生数列”是
的“衍生数列”是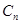 ,….依次将数
,….依次将数
列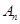 ,
,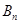 ,
,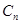 ,…的首项取出,构成数列
,…的首项取出,构成数列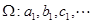 .证明:
.证明: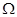 是等差数列.
是等差数列.
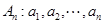 .如果数列
.如果数列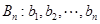 满足
满足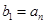 ,
,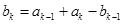 ,其中
,其中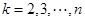 ,则称
,则称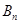 为
为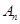 的“衍生数列”.
的“衍生数列”.(Ⅰ)写出数列
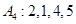 的“衍生数列”
的“衍生数列”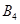 ;
;(Ⅱ)若
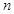 为偶数,且
为偶数,且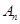 的“衍生数列”是
的“衍生数列”是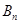 ,证明:
,证明: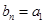 ;
;(Ⅲ)若
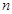 为奇数,且
为奇数,且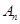 的“衍生数列”是
的“衍生数列”是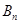 ,
,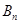 的“衍生数列”是
的“衍生数列”是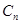 ,….依次将数
,….依次将数列
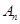 ,
,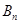 ,
,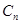 ,…的首项取出,构成数列
,…的首项取出,构成数列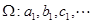 .证明:
.证明: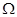 是等差数列.
是等差数列.(Ⅰ)解: . ………………3分
. ………………3分
(Ⅱ)证明: 因为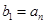 ,
,
 ,
,
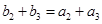 ,
,
……
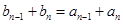 ,
,
由于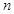 为偶数,将上述
为偶数,将上述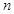 个等式中的第
个等式中的第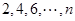 这
这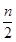 个式子都乘以
个式子都乘以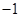 ,相加得
,相加得
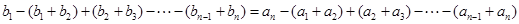 即
即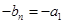 ,
,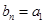 . ………………8分
. ………………8分
(Ⅲ)证明:对于数列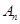 及其“衍生数列”
及其“衍生数列”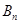 ,
,
因为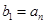 ,
,
 ,
,
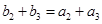 ,
,
……
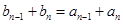 ,
,
由于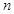 为奇数,将上述
为奇数,将上述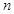 个等式中的第
个等式中的第 这
这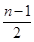 个式子都乘以
个式子都乘以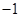 ,
,
相加得
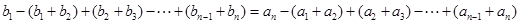 即
即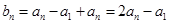 .
.
设数列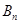 的“衍生数列”为
的“衍生数列”为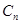 ,
,
因为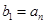 ,
,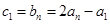 ,
,
所以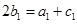 , 即
, 即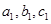 成等差数列. ………………12分
成等差数列. ………………12分
同理可证,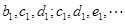 也成等差数列.
也成等差数列.
从而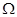 是等差数列. ………………13分
是等差数列. ………………13分
 . ………………3分
. ………………3分(Ⅱ)证明: 因为
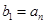 ,
, ,
,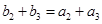 ,
,……
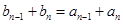 ,
,由于
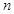 为偶数,将上述
为偶数,将上述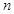 个等式中的第
个等式中的第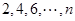 这
这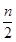 个式子都乘以
个式子都乘以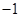 ,相加得
,相加得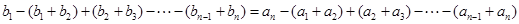 即
即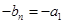 ,
,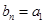 . ………………8分
. ………………8分(Ⅲ)证明:对于数列
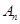 及其“衍生数列”
及其“衍生数列”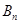 ,
,因为
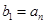 ,
, ,
,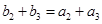 ,
,……
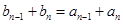 ,
,由于
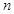 为奇数,将上述
为奇数,将上述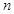 个等式中的第
个等式中的第 这
这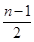 个式子都乘以
个式子都乘以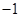 ,
,相加得
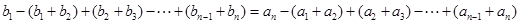 即
即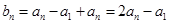 .
.设数列
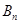 的“衍生数列”为
的“衍生数列”为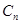 ,
,因为
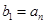 ,
,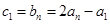 ,
,所以
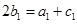 , 即
, 即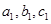 成等差数列. ………………12分
成等差数列. ………………12分同理可证,
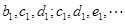 也成等差数列.
也成等差数列.从而
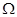 是等差数列. ………………13分
是等差数列. ………………13分略

练习册系列答案
相关题目
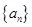 ,
,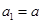 ,且
,且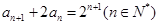 ,
,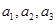 成等差数列,求实数
成等差数列,求实数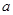 的值;(2)数列
的值;(2)数列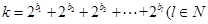 ,且
,且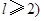 ,求m的最小值.
,求m的最小值.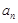 },
},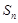 为其前n项的和,
为其前n项的和,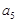 =6,
=6,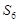 =18,n∈N*.
=18,n∈N*. I)求数列{
I)求数列{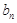 =3
=3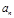 ,求数列{
,求数列{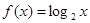 ,若
,若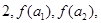
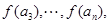
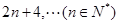 成等差数列.
成等差数列.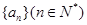 的通项公式;
的通项公式;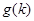 是不等式
是不等式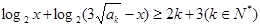 整数解的个数,求
整数解的个数,求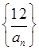 的前n项和为
的前n项和为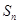 ,是否存在正数
,是否存在正数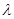 ,对任意正整数
,对任意正整数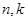 ,使
,使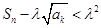 恒成立?若存在,求
恒成立?若存在,求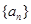 前
前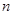 项和为
项和为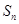 ,若
,若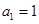 ,
,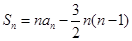 .
.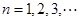
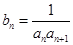 ,数列
,数列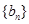 前
前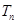 ,证明:
,证明: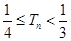 ;
;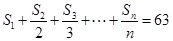 ?若存在,求出
?若存在,求出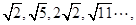 则
则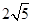 是这个数列的
是这个数列的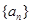 满足性质“对任意正整数
满足性质“对任意正整数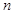 ,
,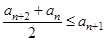 都成立”且
都成立”且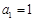 ,
,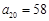 ,则
,则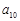 的最小值为
的最小值为 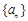 的通项公式
的通项公式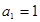
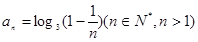 ,设其前
,设其前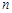 项和为
项和为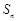 ,则使
,则使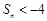 成立的最小自然数
成立的最小自然数