题目内容
已知向量a＝(cos
x，sinx)，b＝(cos
，sin)，c＝(
，－1)，其中x∈R，
(1)当a·b＝
时，求x值的集合；
(2)设函数f(x)＝(a－c)2，求f(x)的最小正周期及其单调增区间.
【解析】(1)∵a·b＝cos
·cos－sinsin＝cos2x＝，
∴2x＝2kπ±
，x＝kπ±
(k∈Z)，
∴x的集合是{x|x＝kπ±(k∈Z)}.
(2)∵a－c＝(cos－，sin＋1)，
∴f(x)＝(cos－)2＋(sin＋1)2＝2＋3－2cos＋2sin
＝5＋4(sin－
cos)＝5＋4sin(－).
①最小正周期T＝
＝
π；
②2kπ－
≤－≤2kπ＋，即2kπ－≤≤2kπ＋
，
kπ－
≤x≤kπ＋
π(k∈Z)，
∴f(x)的单调增区间是[kπ－，kπ＋](k∈Z).
练习册系列答案
阅读快车系列答案
相关题目
，－1)，则|2a－b|的最大值、最小值分别是________．
，－1)，则|2a－b|的最大值是________．
.
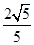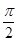<β<0<α<
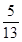，求sinα的值．