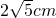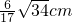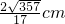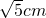题目内容
长为2cm的线段PO⊥面α，O为垂足，A，B是平面α内两动点，若tan∠PAO=
，tan∠PBO=2，则点P与直线AB的距离最大值是（ ）
| 1 |
| 2 |
A．2
| B．
| C．
| D．
|
如图，过O作出OE⊥AB，连接PE，
∵PO⊥平面OAB，∴PO⊥AB，由三垂线定理，可得AB⊥PE，
因为长为2cm的线段PO⊥面α，O为垂足，A，B是平面α内两动点，若tan∠PAO=
| 1 |
| 2 |
所以OB=4，AO=1，
OA≥OE，
当OA=OE时，PE取得最大值，此时PA的长度为PA=
| 22+12 |
| 5 |
故选D．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
，tan∠PBO=2，则点P与直线AB的距离最大值是
