题目内容
下列各点不是函数f(x)=sin(2x-
)+
cos(2x-
)图象的对称中心的是（ ）
| π |
| 3 |
| 3 |
| π |
| 3 |
A、(
| ||
| B、（-π，0） | ||
C、(
| ||
| D、（0，0） |
分析：利用两角和的正弦公式化简函数的解析式为 2sin2x，由2x=kπ，k∈z，可得对称中心的横坐标 x 的值，又纵坐标等于0，可得对称中心的坐标．
解答：解：函数f(x)=sin(2x-
)+
cos(2x-
)=2[
sin(2x-
)+
cos(2x-
)]
=2sin（2x-
+
）=2sin2x．
令2x=kπ，k∈z，可得 x=
，k∈z，故函数图象的对称中心为（
，0），k∈z．
故选C．
| π |
| 3 |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| ||
| 2 |
| π |
| 3 |
=2sin（2x-
| π |
| 3 |
| π |
| 3 |
令2x=kπ，k∈z，可得 x=
| kπ |
| 2 |
| kπ |
| 2 |
故选C．
点评：本题考查两角和的正弦公式，求正弦函数的对称中心，把函数的解析式化为 2sin2x，是解题的关键．
练习册系列答案
相关题目
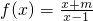的图象是否关于某一点成中心对称？若是，求出对称中心的坐标并说明理由；若不是，请说明理由．
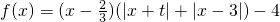的图象关于点
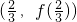成中心对称，求t的值．