题目内容

将4个不相同的小球放入编号为1、2、3的3个盒子中，当某个盒子中球的个数等于该盒子编号时称为一个和谐盒，则恰有两个和谐盒的概率为

A.
$数学公式$
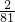
B.
$数学公式$
C.
$数学公式$
D.
$数学公式$

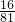
D
分析：根据题意，首先计算4个不同的球放在3个不同的盒子里的其放法数目，再分析恰有2个和谐盒的情况，分：①、1、2号为和谐盒，②、1，3号为和谐盒两种情况讨论，分别计算其情况数目，进而由等可能事件的概率公式，计算可得答案．
解答：根据题意，4个不同的球放在3个不同的盒子里，其放法有3⁴=81种，
恰有2个和谐盒的情况有：①、1、2号为和谐盒，1号盒的放法有4种，2号盒的放法有C₃²=3种，
其放法共有4×3=12种，
②、1，3号为和谐盒，1号盒的放法有4种，剩下3个球放进3号盒中，则3号盒的放法有1种，
其放法共有4种，
所以，恰好有2个和谐盒的概率为 $\text{[math]}$ = $\text{[math]}$ ，
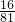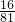故选D．
点评：本题考查等可能事件的概率的计算，关键是明确和谐盒的定义，由排列、组合知识进行计算．

练习册系列答案

某人随机地将编号为1，2，3，4的四个大小相同的小球放入编号为1，2，3，4的四个型号相同的盒子中，每个盒子放一个球，当球的编号与盒子的编号相同时叫做“放法恰当”，否则叫做“放法不恰当”．设放法恰当的情况数为随即变量ξ．
（1）求ξ的分布列；
（2）求ξ的期望与方差．

（本小题满分12分）

一个不透明的袋子中装有4个形状相同的小球，分别标有不同的数字2，3，4，，现从袋中随机摸出2个球，并计算摸出的这2个球上的数字之和，记录后将小球放回袋中搅匀，进行重复试验。记A事件为“数字之和为7”.试验数据如下表

摸球总次数	10	20	30	60	90	120	180	240	330	450
“和为7”出现的频数	1	9	14	24	26	37	58	82	109	150
“和为7”出现的频率	0.10	0.45	0.47	0.40	0.29	0.31	0.32	0.34	0.33	0.33

（参考数据：）

（Ⅰ）如果试验继续下去，根据上表数据，出现“数字之和为7”的频率将稳定在它的概率附近。试估计“出现数字之和为7”的概率，并求的值；

（Ⅱ）在（Ⅰ）的条件下，设定一种游戏规则：每次摸2球，若数字和为7，则可获得奖金7元，否则需交5元。某人摸球3次，设其获利金额为随机变量元，求的数学期望和方差。

有一个不透明的袋子，装有4个完全相同的小球，球上分别编有数字1，2，3，4．
（Ⅰ）若逐个不放回取球两次，求第一次取到球的编号为偶数且两个球的编号之和能被3整除的概率；
（Ⅱ）若先从袋中随机取一个球，该球的编号为a，将球放回袋中，然后再从袋中随机取一个球，该球的编号为b，求直线ax+by+1=0与圆x²+y²=

有公共点的概率．

将4个不相同的小球放入编号为1、2、3的3个盒子中，当某个盒子中球的个数等于该盒子编号时称为一个和谐盒，则恰有两个和谐盒的概率为

试题分类