题目内容
设函数
的零点为
的零点为
，若
可以是
A． | B． |
C． | D． |
D
解析试题分析：对于A，f(x)的零点为1或-1，则根据题意g(x)的零点在区间
或
，又函数g(x)是单调递增函数，且
，故这两个区间都不存在零点；
对于B，f(x)的零点2，则根据题意g(x)的零点在区间
，根据A中可知，不正确；
对于C，f(x)的零点为0，则根据题意g(x)的零点在区间
，又
，
故不正确；
对于D，f(x)的零点为
，则根据题意g(x)的零点在区间
，又
，
所以正确，故选D
考点：本题考查函数的零点，零点存在性定理
点评：解决本题的关键是掌握零点存在性定理，结合函数的单调性
练习册系列答案
相关题目
已知m∈R，“函数
有零点”是“函数
在（0，+∞）上为减函数”的（ ）
| A．充分不必要条件 |
| B．必要不充分条件 |
| C．充要条件 |
| D．既不充分也不必要条件 |
命题“
，
”的否定是（ ）
A．, | B． , |
C．， | D．， |
下列命题中真命题的个数是（ ）
①?x∈R，x4>x2；
②若p∧q是假命题，则p，q都是假命题；
③命题“?x∈R，x3－x2＋1≤0”的否定是“?x∈R，x3－x2＋1>0”．
| A．0 | B．1 | C．2 | D．3 |
，
”的否定是_____________.若
，则
（ ）
A． | B． | C． | D． |
若
，则
（ ）
A． | B． | C． | D． |
若
，则
（ ）
| A．2 | B．2或-2 | C． | D．-2 |
设
,若
是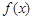
的最小值,则
的取值范围为（ ）
| A．[-1,2] | B．[-1,0] | C．[1,2] | D．[0,2] |