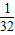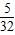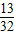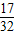题目内容
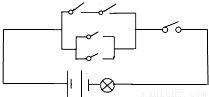 以下电路中,每个开关闭合的概率均为
以下电路中,每个开关闭合的概率均为 ,且相互独立,则电灯亮的概率为( )
,且相互独立,则电灯亮的概率为( )A.
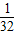
B.
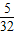
C.
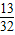
D.
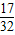
【答案】分析:所有的情况共有25种,而灯亮的情况有:①闭合2个开关有2种方法,②闭合3个开关有6种方法,③闭合4个开关有4种方法,④闭合5个开关有1种方法,由此求得灯亮的概率
解答:解:共有5个开关,每个开关都有闭合与断开2种状态,故所有的情况共有25=32种,
而灯亮的情况有:①闭合2个开关有2种方法,②闭合3个开关有6种方法,③闭合4个开关有4种方法,④闭合5个开关有1种方法,
故灯亮的概率为 =
= ,
,
故选C.
点评:本题主要考查相互独立事件的概率乘法公式,体现了分类讨论的数学思想,属于重档题.
解答:解:共有5个开关,每个开关都有闭合与断开2种状态,故所有的情况共有25=32种,
而灯亮的情况有:①闭合2个开关有2种方法,②闭合3个开关有6种方法,③闭合4个开关有4种方法,④闭合5个开关有1种方法,
故灯亮的概率为
 =
= ,
,故选C.
点评:本题主要考查相互独立事件的概率乘法公式,体现了分类讨论的数学思想,属于重档题.

练习册系列答案
相关题目
 以下电路中,每个开关闭合的概率均为
以下电路中,每个开关闭合的概率均为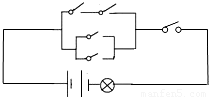 以下电路中,每个开关闭合的概率均为
以下电路中,每个开关闭合的概率均为 ,且相互独立,则电灯亮的概率为( )
,且相互独立,则电灯亮的概率为( )