题目内容
下列命题中,真命题是________.
①?x∈R,使得sinx+cosx=2;
②?x∈(0,π)有sinx>cosx;
③??∈R,使得f(x)=sin(ωx+ω)为奇函数;
④?a∈(-1,0),有 .
.
③④
分析:根据正弦型函数的值域,我们可以判定①的真假;根据正弦函数、余弦函数的图象与性质,我们可以判断②的真假;根据正弦型函数的奇偶性,我们可以判断③的真假;根据不等式的基本性质,可以判断④的真假,进而得到答案.
解答:∵sinx+cosx= sin(x+
sin(x+ )∈[-
)∈[- ,
, ],故①错误;
],故①错误;
当x∈(0, ]时,sinx≤cosx,故②错误;
]时,sinx≤cosx,故②错误;
当φ=kπ,k∈Z时,f(x)=sin(ωx+φ)为奇函数,故③正确;
④当a∈(-1,0)时,a(a2+a+1)<0,即有a3+a2+a+1<1,则 ,故④正确;
,故④正确;
故答案为:③④
点评:本题考查的知识点是正弦型函数的值域,正弦型函数的奇偶性,不等式的性质,全称命题和特特命题,如何判断全(特)称命题的真假,是解答本题的关键.
分析:根据正弦型函数的值域,我们可以判定①的真假;根据正弦函数、余弦函数的图象与性质,我们可以判断②的真假;根据正弦型函数的奇偶性,我们可以判断③的真假;根据不等式的基本性质,可以判断④的真假,进而得到答案.
解答:∵sinx+cosx=
 sin(x+
sin(x+ )∈[-
)∈[- ,
, ],故①错误;
],故①错误;当x∈(0,
 ]时,sinx≤cosx,故②错误;
]时,sinx≤cosx,故②错误;当φ=kπ,k∈Z时,f(x)=sin(ωx+φ)为奇函数,故③正确;
④当a∈(-1,0)时,a(a2+a+1)<0,即有a3+a2+a+1<1,则
 ,故④正确;
,故④正确;故答案为:③④
点评:本题考查的知识点是正弦型函数的值域,正弦型函数的奇偶性,不等式的性质,全称命题和特特命题,如何判断全(特)称命题的真假,是解答本题的关键.

练习册系列答案
相关题目
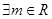 ,使函数
,使函数 是偶函数
是偶函数 ,使函数
,使函数 ≤0
≤0 =-1
=-1