题目内容
(本小题满分12分)
已知点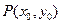 是椭圆
是椭圆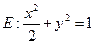 上任意一点
上任意一点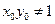 ,直线
,直线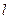 的方程为
的方程为
(I)判断直线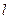 与椭圆E交点的个数;
与椭圆E交点的个数;
(II)直线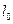 过P点与直线
过P点与直线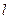 垂直,点M(-1,0)关于直线
垂直,点M(-1,0)关于直线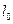 的对称点为N,直线PN恒
的对称点为N,直线PN恒
过一定点G,求点G的坐标。
已知点
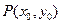 是椭圆
是椭圆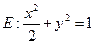 上任意一点
上任意一点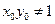 ,直线
,直线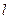 的方程为
的方程为
(I)判断直线
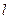 与椭圆E交点的个数;
与椭圆E交点的个数;(II)直线
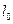 过P点与直线
过P点与直线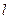 垂直,点M(-1,0)关于直线
垂直,点M(-1,0)关于直线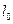 的对称点为N,直线PN恒
的对称点为N,直线PN恒过一定点G,求点G的坐标。
(1)故直线
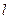 与椭圆
与椭圆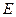 只有一个交点…
只有一个交点…(2)
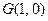
解:(1)由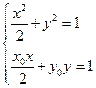 消去
消去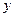 并整理得
并整理得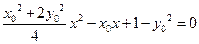 ……2分
……2分
 ,
,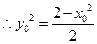
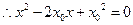 …………4分
…………4分
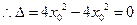
故直线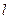 与椭圆
与椭圆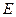 只有一个交点…………5分
只有一个交点…………5分
(2)直线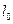 的方程为
的方程为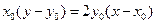
即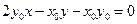 ………………6分
………………6分
设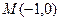 关于直线
关于直线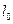 的对称点
的对称点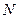 的坐标为
的坐标为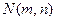
则 解得
解得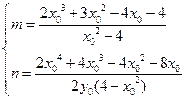 ……8分
……8分
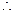 直线
直线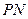 的斜率为
的斜率为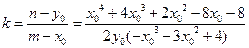
从而直线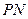 的方程为
的方程为
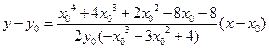
即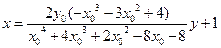
从而直线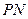 恒过定点
恒过定点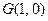 …………12分
…………12分
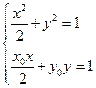 消去
消去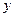 并整理得
并整理得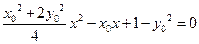 ……2分
……2分 ,
,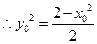
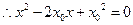 …………4分
…………4分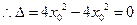
故直线
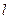 与椭圆
与椭圆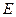 只有一个交点…………5分
只有一个交点…………5分(2)直线
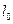 的方程为
的方程为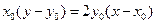
即
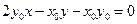 ………………6分
………………6分设
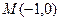 关于直线
关于直线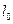 的对称点
的对称点 的坐标为
的坐标为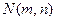
则
 解得
解得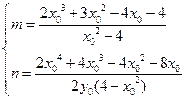 ……8分
……8分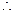 直线
直线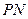 的斜率为
的斜率为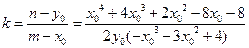
从而直线
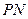 的方程为
的方程为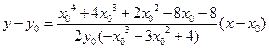
即
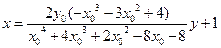
从而直线
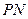 恒过定点
恒过定点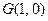 …………12分
…………12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
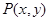 满足椭圆方程
满足椭圆方程 ,则
,则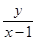 的最大值为(***)
的最大值为(***)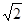
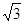
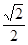
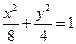 ,直线
,直线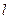 过点P
过点P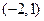 交椭圆C于A、B两点.
交椭圆C于A、B两点.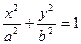 (a>b>0)
(a>b>0) ,一条准线方程为x=4 时,求椭圆方程;
,一条准线方程为x=4 时,求椭圆方程;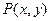 是椭圆上一点,在(1)的条件下,求
是椭圆上一点,在(1)的条件下,求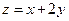 的最大值及相应的P点坐标。
的最大值及相应的P点坐标。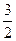 ,BC=
,BC=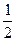 .椭圆C以A、B为焦点且经过点D.
.椭圆C以A、B为焦点且经过点D.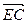
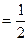
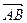 ,问是否存在不平行AB的直线l与椭圆C交于M、N两点且
,问是否存在不平行AB的直线l与椭圆C交于M、N两点且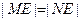 ,若存在,求出直线l与AB夹角的范围,若不存在,说明理由
,若存在,求出直线l与AB夹角的范围,若不存在,说明理由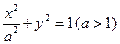 的两个焦点为F1,F2,P为椭圆上一点,且∠F1PF2=60°,则|PF1|·|PF2|的值为
的两个焦点为F1,F2,P为椭圆上一点,且∠F1PF2=60°,则|PF1|·|PF2|的值为 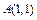 是
是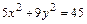 内一点,
内一点,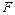 是椭圆的左焦点,点
是椭圆的左焦点,点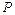 在椭圆上,则
在椭圆上,则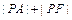 的最大值为 ,最小值为
的最大值为 ,最小值为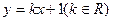 与椭圆
与椭圆

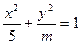 恒有公共点。则实数m的取值范围是( )
恒有公共点。则实数m的取值范围是( )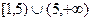
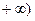
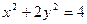 ,则以
,则以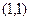 为中点的弦的长度为
为中点的弦的长度为