题目内容
已知函数f（x）=4sin2（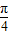
+x）-2
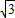cos2x-1．（
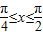）（1）求f（x）的最大值及最小值；
（2）若不等式|f（x）-m|＜2恒成立，求实数m的取值范围．
【答案】分析：（1）首先化简函数为f（x）=4sin（2x-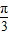
）+1，然后由x的范围得出2x-
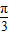的范围，进而由正弦函数的特点求得最值；
（2）首先化简绝对值得出m-2＜f（x）＜m+2，再由恒成立得出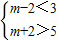
，解出m即可．
解答：解：（1）∵f（x）=2[1-cos（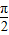
+2x）]-2
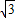cos2x-1=2sin2x-2
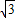cos2x+1=4sin（2x-
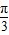）+1
又∵
∴
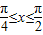
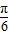≤2x-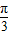
≤
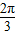
即3≤4sin（2x-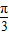
）+1≤5
∴ymax=5，ymin=3
（2）∵|f（x）-m|＜2
m-2＜f（x）＜m+2
∴
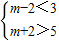解得3＜m＜5
即所求的m的取值范围是（3，5）
当m+3＜0即m＜-3时，x∈R
点评：此题考查了二倍角公式、两角和与差公式、正弦函数的特点以及恒成立问题，正确化简函数解析式是解题的关键，属于中档题．
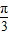）+1，然后由x的范围得出2x-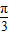的范围，进而由正弦函数的特点求得最值；（2）首先化简绝对值得出m-2＜f（x）＜m+2，再由恒成立得出
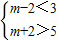，解出m即可．解答：解：（1）∵f（x）=2[1-cos（
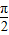+2x）]-2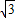cos2x-1=2sin2x-2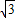cos2x+1=4sin（2x-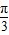）+1又∵
∴
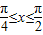
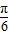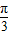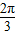
≤2x-≤即3≤4sin（2x-
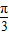）+1≤5∴ymax=5，ymin=3
（2）∵|f（x）-m|＜2
m-2＜f（x）＜m+2
∴
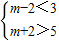解得3＜m＜5即所求的m的取值范围是（3，5）
当m+3＜0即m＜-3时，x∈R
点评：此题考查了二倍角公式、两角和与差公式、正弦函数的特点以及恒成立问题，正确化简函数解析式是解题的关键，属于中档题．
练习册系列答案
相关题目