题目内容
过点(0,1)与圆x2+y2-2x=0相切的直线方程为________.
x=0或y=1
分析:把圆的方程化为标准方程,找出圆心坐标和半径r,根据题意画出图形,显然y轴于已知圆相切;设出切线的斜率为k,根据切线过已知点表示出出切线方程,因为直线与圆相切,所以圆心到直线的距离d等于半径r,故利用点到直线的距离公式表示出d,让d等于r列出关于k的方程,求出方程的解即可确定出切线方程,综上得到两条满足题意的切线方程.
解答: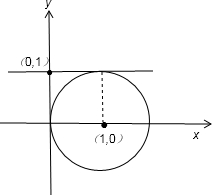
解:把圆的方程x2+y2-2x=0化为标准方程得:(x-1)2+y2=1,
所以圆心坐标为(1,0),半径r=1,
显然圆与y轴相切,且(0,1)在y轴上,故过(0,1)的直线y轴于圆相切,此时切线方程为x=0;
设切线的斜率为k,由切线过(0,1),得到切线方程为:y-1=k(x-0),即y=kx+1,
则有圆心到切线的距离d=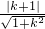 =r=1,解得k=0,
=r=1,解得k=0,
所以切线方程为:y=1,
综上,所求切线的方程为x=0或y=1.
故答案为:x=0或y=1
点评:此题考查了直线与圆相切满足的关系,考查了数形结合的思想,掌握当直线与圆相切时,圆心到直线的距离等于圆的半径是解本题的关键,同时要求学生灵活运用点到直线的距离公式,会把圆的方程化为标准方程,会从圆的标准方程找出圆心坐标和圆的半径,此外满足题意的切线有两条,做题时不要漏解.
分析:把圆的方程化为标准方程,找出圆心坐标和半径r,根据题意画出图形,显然y轴于已知圆相切;设出切线的斜率为k,根据切线过已知点表示出出切线方程,因为直线与圆相切,所以圆心到直线的距离d等于半径r,故利用点到直线的距离公式表示出d,让d等于r列出关于k的方程,求出方程的解即可确定出切线方程,综上得到两条满足题意的切线方程.
解答:

解:把圆的方程x2+y2-2x=0化为标准方程得:(x-1)2+y2=1,
所以圆心坐标为(1,0),半径r=1,
显然圆与y轴相切,且(0,1)在y轴上,故过(0,1)的直线y轴于圆相切,此时切线方程为x=0;
设切线的斜率为k,由切线过(0,1),得到切线方程为:y-1=k(x-0),即y=kx+1,
则有圆心到切线的距离d=
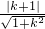 =r=1,解得k=0,
=r=1,解得k=0,所以切线方程为:y=1,
综上,所求切线的方程为x=0或y=1.
故答案为:x=0或y=1
点评:此题考查了直线与圆相切满足的关系,考查了数形结合的思想,掌握当直线与圆相切时,圆心到直线的距离等于圆的半径是解本题的关键,同时要求学生灵活运用点到直线的距离公式,会把圆的方程化为标准方程,会从圆的标准方程找出圆心坐标和圆的半径,此外满足题意的切线有两条,做题时不要漏解.

练习册系列答案
相关题目
 已知椭圆
已知椭圆