题目内容
2.光点随机出现在圆C1:4x2+4y2=π2的内部,则光点出现曲线C2:y2-cos2x=0,x∈[-$\frac{π}{2}$,$\frac{π}{2}$]内部的概率为$\frac{16}{{π}^{3}}$.分析 由题意,分别画出圆C1:4x2+4y2=π2和曲线C2:y2-cos2x=0,x∈[-$\frac{π}{2}$,$\frac{π}{2}$]的图形,由几何概型公式得到所求为两部分的面积比.
解答 解:由题意圆C1:4x2+4y2=π2的内部,曲线C2:y2-cos2x=0,x∈[-$\frac{π}{2}$,$\frac{π}{2}$]表示的区域如图所示,
根据几何概型公式可得光点出现曲线C2:y2-cos2x=0,x∈[-$\frac{π}{2}$,$\frac{π}{2}$]内部的概率为:$\frac{4{∫}_{0}^{\frac{π}{2}}cosxdx}{π\frac{{π}^{2}}{4}}$=$\frac{16}{{π}^{3}}$;
故答案为:$\frac{16}{{π}^{3}}$.
点评 本题考查了几何概型公式的运用;关键是明确所求为两部分的面积比.

练习册系列答案
 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
13.已知命题p:函数y=f(x)在区间[a,b]上单调递增,命题q:函数y=f(x)单调递增区间为[a,b],则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
10.某篮球架的底座三视图如图所示,则其体积为( )


| A. | $\frac{{470+10\sqrt{30}}}{3}$ | B. | 175 | C. | 180 | D. | 295+10$\sqrt{2}$ |
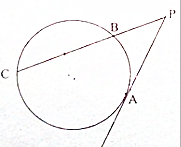 如图,PA是圆的切线,A为切点,PBC是圆的割线,且PB=$\frac{1}{2}$BC,则$\frac{PA}{PB}$=$\sqrt{3}$.
如图,PA是圆的切线,A为切点,PBC是圆的割线,且PB=$\frac{1}{2}$BC,则$\frac{PA}{PB}$=$\sqrt{3}$.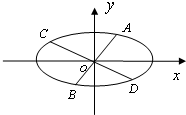 椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的经过中心的弦称为椭圆的一条直径,平行于该直径的所有弦的中点的轨迹为一条直线段,称为该直径的共轭直径.已知椭圆的方程为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1
椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的经过中心的弦称为椭圆的一条直径,平行于该直径的所有弦的中点的轨迹为一条直线段,称为该直径的共轭直径.已知椭圆的方程为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1