题目内容
用反证法证明：函数f（x）=x3-2x2-5x+6在区间（3，+∞）上不存在极值点．
分析：假设函数f（x）=x3-2x2-5x+6在区间（3，+∞）上存在极值点，令f'（x）=0可得导函数的零点，下面证明这两个零点都不在区间（3，+∞）上即可，最后得到与假设矛盾，故假设不成立，从而得到证明．
解答：22．证明：假设函数f（x）=x3-2x2-5x+6在区间（3，+∞）上存在极值点． …1分
则存在x0＞3，使得f'（x0）=0． …2分
因为f'（x）=3x2-4x-5，令f'（x）=0，则x=
． …3分
容易看出
＜3，下面证明
＜3． …4分
要证明：
＜3成立，
只需证：2+
＜9成立，
只需证：
＜7成立，
只需证：19＜49成立，
上式显然成立，故有
＜3成立．
综上，x=
＜3，与存在x0＞3，使得f'（x0）=0矛盾． …7分
因此假设不成立，所以函数f（x）=x3-2x2-5x+6在区间（3，+∞）上不存在极值点．…8分．
则存在x0＞3，使得f'（x0）=0． …2分
因为f'（x）=3x2-4x-5，令f'（x）=0，则x=
2±
| ||
| 3 |
容易看出
2-
| ||
| 3 |
2+
| ||
| 3 |
要证明：
2+
| ||
| 3 |
只需证：2+
| 19 |
只需证：
| 19 |
只需证：19＜49成立，
上式显然成立，故有
2+
| ||
| 3 |
综上，x=
2±
| ||
| 3 |
因此假设不成立，所以函数f（x）=x3-2x2-5x+6在区间（3，+∞）上不存在极值点．…8分．
点评：本题主要考查用反证法证明数学命题，推出矛盾，是解题的关键和难点，属于中档题．
练习册系列答案
相关题目
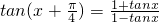；②用反证法证明：函数f（x）=tanx的最小正周期是π；
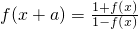，试问：f（x）是周期函数吗？证明你的结论．