题目内容
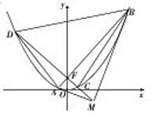
(本小题满分12分)已知抛物线![]() 的焦点为
的焦点为![]() ,过焦点
,过焦点![]() 且不平行于
且不平行于![]() 轴的动直线
轴的动直线![]() 交抛物线于A、B两点,抛物线在A、B两点处的切线交于点M。
交抛物线于A、B两点,抛物线在A、B两点处的切线交于点M。
(1)求证:A、M、B三点的横坐标成等差数列;
(2)设直线![]() 交该抛物线于C、D两点,求四边形ACBD面积的最小值。
交该抛物线于C、D两点,求四边形ACBD面积的最小值。
解:(1)由已知得![]() ,显然直线
,显然直线![]() 的斜率存在且不为0,可设直线
的斜率存在且不为0,可设直线![]() 的方程为:
的方程为:
![]() ,
,![]()
由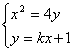 得
得![]() ,显然
,显然![]()
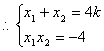
由![]() 得
得![]() ,
,
![]()
直线![]() 的斜率为
的斜率为![]()
直线![]() 的方程为直线
的方程为直线![]()
化简得![]() 的方程为
的方程为![]()
同理可得直线![]() 的方程为
的方程为![]()
两式相减得![]()
即![]() 三点的横坐标成等差数列。
三点的横坐标成等差数列。
(2)由(1)知![]()
点![]() 的坐标为
的坐标为![]()
![]()
则直线![]() 的方程为:
的方程为:![]()
设![]()
由 得:
得:![]() ,显然
,显然![]()
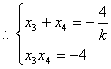
![]()
![]()
![]()
![]()
![]()
当且仅当![]() 时,四边形
时,四边形![]() 的面积有最小值32.
的面积有最小值32.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目