题目内容
已知f(x)＝
(a，b，c∈N)是奇函数，且f(1)＝2，f(2)＜3，求a，b，c的值．
答案：
解析：
解析：
分析：要求参数就要建立等式或建立有限制条件的不等式．f(x)是奇函数，则有f(－x)＝－f(x)．又f(1)＝2，且f(2)＜3，结合a，b，c∈N即可得解．
解：由f(x)是奇函数，知f(－x)＝－f(x)，即
＝－
＝，比较系数得c＝0，则f(x)＝
，且b≠0．
由f(1)＝2，得a＋1＝2b．由f(2)＜3，及b∈N+，得4a＋1＜6b＝3(a＋1)，即a＜2，又a∈N，所以a＝1或0．当a＝1时，b＝1；当a＝0时，b＝
N，所以a＝1，b＝1，c＝0．
点评：解本题的关键是根据奇函数的定义建立等式．
练习册系列答案
相关题目
) (a
(a＞0且a≠1)，确定函数的奇偶性、单调性．
是定义在R上的奇函数，则f－1(－
)的值是
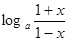(a＞0,a≠1)