题目内容
同时具有性质“①最小正周期是
；②图象关于直线
对称；③在
上是增函数”的 一个函数是（ ）.
A． | B． |
C． | D． |
C
解析试题分析：由于周期
，排除
，图象关于直线
对称，排除
,由于
，
因此
满足三个性质.
考点：正弦型函数的性质.
练习册系列答案
相关题目
“三角函数是周期函数，y＝tanx，x∈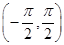
是三角函数，所以y＝tan x，
x∈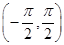是周期函数．”在以上演绎推理中，下列说法正确的是( )．
| A．推理完全正确 | B．大前提不正确 |
| C．小前提不正确 | D．推理形式不正确 |
已知点
，
在第二象限，则
的一个变化区间是
A． | B． | C． | D． |
已知
，那么角
是（ ）
| A．第一或第二象限角 | B．第二或第三象限角 |
| C．第三或第四象限角 | D．第一或第四象限角 |
要得到f(x)＝tan
的图象，只须将f(x)＝tan2x的图象( )
A．向右平移 个单位 | B．向左平移个单位 |
C．向左平移 个单位 | D．向右平移个单位 |
已知函数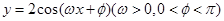
满足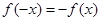
，其图像与直线y=0的某两个交点的横坐标分别为
、
,
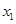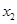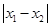的最小值为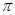
，则（ ）.
A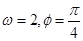． | B． | C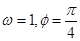． | D． |
函数
的部分图象如图所示，则
的值是（ ）.
| A．0 | B．－1 | C．2＋2 | D．2－2 |
已知角
的始边与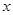
轴非负半轴重合，终边在直线
上，则
（ ）
A． | B． | C． | D． |
设函数f(x)=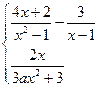
在点x=1处连续，则a等于
A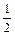．- | B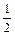． | C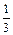．- | D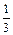． |