题目内容
已知函数f(x)=ax-1-lnx(a∈R).(1)讨论函数f(x)在定义域内的极值点的个数;
(2)若函数f(x)在x=1处取得极值,对?x∈(0,+∞),f(x)≥bx-2恒成立,求实数b的取值范围;
(3)当x>y>e-1时,求证:
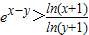 .
.
【答案】分析:(Ⅰ)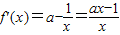 ,由此进行分类讨论,能求出函数f(x)在定义域内的极值点的个数.
,由此进行分类讨论,能求出函数f(x)在定义域内的极值点的个数.
(Ⅱ)由函数f(x)在x=1处取得极值,知a=1,故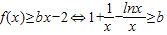 ,由此能求出实数b的取值范围.
,由此能求出实数b的取值范围.
(Ⅲ)由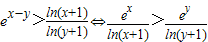 ,令
,令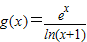 ,则只要证明g(x)在(e-1,+∞)上单调递增,由此能够证明
,则只要证明g(x)在(e-1,+∞)上单调递增,由此能够证明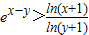 .
.
解答:解:(Ⅰ)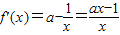 ,
,
当a≤0时,f'(x)<0在(0,+∞)上恒成立,
函数f(x)在(0,+∞)单调递减,
∴f(x)在(0,+∞)上没有极值点;
当a>0时,f'(x)<0得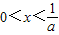 ,f'(x)>0得
,f'(x)>0得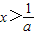 ,
,
∴f(x)在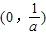 上递减,在
上递减,在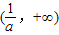 上递增,
上递增,
即f(x)在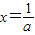 处有极小值.
处有极小值.
∴当a≤0时f(x)在(0,+∞)上没有极值点,
当a>0时,f(x)在(0,+∞)上有一个极值点.(4分)
(注:分类讨论少一个扣一分.)
(Ⅱ)∵函数f(x)在x=1处取得极值,∴a=1,…(5分)
∴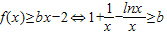 ,…(6分)
,…(6分)
令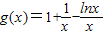 ,可得g(x)在(0,e2]上递减,在[e2,+∞)上递增,…(8分)
,可得g(x)在(0,e2]上递减,在[e2,+∞)上递增,…(8分)
∴ ,即
,即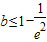 .(9分)
.(9分)
(Ⅲ)证明: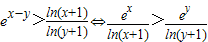 ,(10分)
,(10分)
令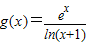 ,
,
则只要证明g(x)在(e-1,+∞)上单调递增,
又∵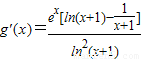 ,
,
显然函数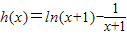 在(e-1,+∞)上单调递增.(12分)
在(e-1,+∞)上单调递增.(12分)
∴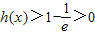 ,即g'(x)>0,
,即g'(x)>0,
∴g(x)在(e-1,+∞)上单调递增,
即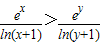 ,
,
∴当x>y>e-1时,有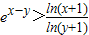 .(14分)
.(14分)
点评:本题考查函数的求极值点的个数的求法,考查满足条件的实数的求法,考查不等式的证明.解题时要合理运用导数性质,注意等价转化思想和分类讨论思想的灵活运用.
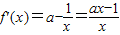 ,由此进行分类讨论,能求出函数f(x)在定义域内的极值点的个数.
,由此进行分类讨论,能求出函数f(x)在定义域内的极值点的个数.(Ⅱ)由函数f(x)在x=1处取得极值,知a=1,故
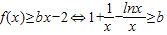 ,由此能求出实数b的取值范围.
,由此能求出实数b的取值范围.(Ⅲ)由
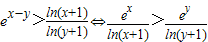 ,令
,令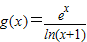 ,则只要证明g(x)在(e-1,+∞)上单调递增,由此能够证明
,则只要证明g(x)在(e-1,+∞)上单调递增,由此能够证明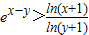 .
.解答:解:(Ⅰ)
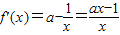 ,
,当a≤0时,f'(x)<0在(0,+∞)上恒成立,
函数f(x)在(0,+∞)单调递减,
∴f(x)在(0,+∞)上没有极值点;
当a>0时,f'(x)<0得
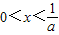 ,f'(x)>0得
,f'(x)>0得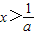 ,
,∴f(x)在
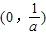 上递减,在
上递减,在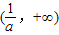 上递增,
上递增,即f(x)在
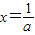 处有极小值.
处有极小值.∴当a≤0时f(x)在(0,+∞)上没有极值点,
当a>0时,f(x)在(0,+∞)上有一个极值点.(4分)
(注:分类讨论少一个扣一分.)
(Ⅱ)∵函数f(x)在x=1处取得极值,∴a=1,…(5分)
∴
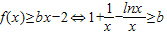 ,…(6分)
,…(6分)令
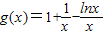 ,可得g(x)在(0,e2]上递减,在[e2,+∞)上递增,…(8分)
,可得g(x)在(0,e2]上递减,在[e2,+∞)上递增,…(8分)∴
 ,即
,即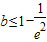 .(9分)
.(9分)(Ⅲ)证明:
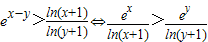 ,(10分)
,(10分)令
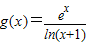 ,
,则只要证明g(x)在(e-1,+∞)上单调递增,
又∵
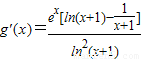 ,
,显然函数
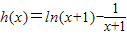 在(e-1,+∞)上单调递增.(12分)
在(e-1,+∞)上单调递增.(12分)∴
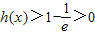 ,即g'(x)>0,
,即g'(x)>0,∴g(x)在(e-1,+∞)上单调递增,
即
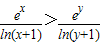 ,
,∴当x>y>e-1时,有
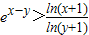 .(14分)
.(14分)点评:本题考查函数的求极值点的个数的求法,考查满足条件的实数的求法,考查不等式的证明.解题时要合理运用导数性质,注意等价转化思想和分类讨论思想的灵活运用.

练习册系列答案
相关题目