题目内容
计算下列几个式子，①tan25°+tan35°+
tan25°tan35°，②2（sin35°cos25°+sin55°cos65°），
③
，④
，结果为
的是（ ）A．①②
B．③
C．①②③
D．②③④
【答案】分析：先令tan60°=tan（25°+35°）利用正切的两角和公式化简整理求得tan25°+tan35°=
（1-tan25°tan35°），整理后求得tan25°+tan35°+
tan25°tan35°=
；②中利用诱导公式把sin55°转化才cos35°，cos65°转化为sin25°，进而利用正弦的两角和公式整理求得结果为
；③中利用正切的两角和公式求得原式等于tan60°，结果为
，④中利用正切的二倍角公式求得原式等于
，推断出④不符合题意．
解答：解：∵tan60°=tan（25°+35°）=
=
∴tan25°+tan35°=
（1-tan25°tan35°）
∴tan25°+tan35°+
tan25°tan35°=
，①符合
2（sin35°cos25°+sin55°cos65°）=2（sin35°cos25°+cos35°sin25°）=2sin60°=
，②符合
=tan（45°+15°）=tan60°=
，③符合
=
=
tan
=
，④不符合
故结果为
的是①②③
故选C
点评：本题主要考查了三角函数的化简求值，两角和公式的应用和二倍角公式的应用．考查了学生对三角函数基础公式的理解和灵活一运用．
（1-tan25°tan35°），整理后求得tan25°+tan35°+tan25°tan35°=；②中利用诱导公式把sin55°转化才cos35°，cos65°转化为sin25°，进而利用正弦的两角和公式整理求得结果为；③中利用正切的两角和公式求得原式等于tan60°，结果为，④中利用正切的二倍角公式求得原式等于，推断出④不符合题意．解答：解：∵tan60°=tan（25°+35°）=
=∴tan25°+tan35°=
（1-tan25°tan35°）∴tan25°+tan35°+
tan25°tan35°=，①符合2（sin35°cos25°+sin55°cos65°）=2（sin35°cos25°+cos35°sin25°）=2sin60°=
，②符合=tan（45°+15°）=tan60°=，③符合==tan=，④不符合故结果为
的是①②③故选C
点评：本题主要考查了三角函数的化简求值，两角和公式的应用和二倍角公式的应用．考查了学生对三角函数基础公式的理解和灵活一运用．
练习册系列答案
相关题目
，
， 
，
的是 （填上所有你认为正确答案的序号）
,
, 
，
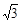的是（
）