Question

【题目】如图，F1、F2为双曲线C：的左、右焦点，动点P(x0，y0)(y0≥1)在双曲线C的右支上.设∠F1PF2的平分线与x轴、y轴分别交于点M(m，0)、N.

（1）求m的取值范围；

（2）设过点F1、N的直线l与双曲线C交于D、E两点，求△F2DE面积的最大值.

Answer 1

【答案】(1) (0，]. (2) 4

【解析】

（1）依题意有F1(-，0)，F2(，0).

则

，

.

由点M在∠F1PF2的平分线上知

.

由，y0≥1及

.

则，

.

故.

结合x0≥2.

从而，m的取值范围是(0，].

（2）由（1）知

.

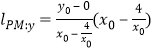令x=0 .

故点.

由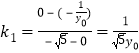

.

与双曲线方程联立消去x得

①

.

设D(x1，y1)，E(x2，y2). 1

则，

.

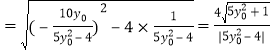由y0≥1，知.

设.于是，t≥1.

故.

当t=1，即点P(2，1)时，△F2DE面积取最大值4 .

从而，△F2DE面积的最大值为4.