Question

已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜

π

2

）的图象在y轴上的截距为1，在相邻最值点（x₀，2），[x₀+

3

2

，-2]（x₀＞0）上f（x）分别取得最大值和最小值．
（1）求f（x）的解析式；
（2）求方程f（x）=a存在于[0，7/2]上的解的和，其中a为满足-2＜a＜2的已知常数．

Answer 1

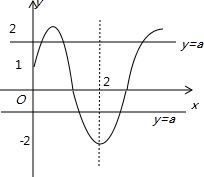
分析：（1）由题意求出A，T再求ω，利用图象过（0，1）求出φ，求f（x）的解析式；
（2）求方程f（x）=a存在于[0，7/2]上的解的和，其中a为满足-2＜a＜2的已知常数．需要分类：-2＜a＜1时1≤a＜2，借助图象，利用对称性、以及三角方程解答即可．

解答：解：（1）函数f（x）=Asin（ω+φ）（A＞0，ω＞0，|φ|＜

π

2

）的图象在y轴上的截距为1，
在相邻最值点（x₀，2），[x₀+

3

2

，-2]（x₀＞0）上f（x）分别取得最大值和最小值．
所以A=2，T=3，ω=

2π

3

，（0，1）在函数图象上，
所以1=2sinφ，φ=

π

6

所以函数的解析式：f(x)=2sin(

2π

3

x+

π

6

)
（2）当-2＜a＜1时，方程f（x）=a存在于[0，

7

2

]上的解的和为4，
当1≤a＜2时：由2sin(

2π

3

x+

π

6

)=a
解得x=

3

2π

arcsin

a

2

-

π

6

=

3

2π

arcsin

a

2

-

π

6

×

3

2π

 解的和为：

15

4

+

3

2π

arcsin

a

2

点评：本题考查三角函数的周期性及其求法，三角函数的最值，函数的解析式，考查计算能力，视图能力，是基础题．