题目内容
已知定义域为R的奇函数f(x)=| -2x+b | 2x+1+a |
(Ⅰ)求a,b的值
(Ⅱ)判定函数f(x)的单调性,并用定义证明.
分析:(Ⅰ)由题意知f(0)=0求出b,再由奇函数的定义求出b;
(Ⅱ)先用分离常数法将解析式化简后判断出单调性,再用定义证明即:取值、作差、变形、判断符 号、得出结论.
(Ⅱ)先用分离常数法将解析式化简后判断出单调性,再用定义证明即:取值、作差、变形、判断符 号、得出结论.
解答:解:(Ⅰ)∵f(x)是R上奇函数
由f(0)=0即
=0得b=1(1分)
又由f(-x)=-f(x)即
=-
,解得a=2(5分)
(Ⅱ)由f(x)=
=
-
(6分)
∵2x为增函数,∴f(x)是R上的减函数(7分)
证明:设x1<x2,f(x1)-f(x2)=
-
=
(10分)
∵x1<x2∴2x1<2x22x2-2x1>0(11分)
∵2x1+1>0,2x2+1>0∴
>0
∴f(x1)-f(x2)>0,∴f(x1)>f(x2)(12分)
∴f(x)是R上的减函数(13分)
由f(0)=0即
| -1+b |
| 2+a |
又由f(-x)=-f(x)即
| -2-x+1 |
| 2-x+1+a |
| -2x+1 |
| 2x+1+a |
(Ⅱ)由f(x)=
| -2x+1 |
| 2x+1+2 |
| 1 |
| 2x+1 |
| 1 |
| 2 |
∵2x为增函数,∴f(x)是R上的减函数(7分)
证明:设x1<x2,f(x1)-f(x2)=
| 1 |
| 2x1+1 |
| 1 |
| 2x2+1 |
| 2x2-2x1 |
| (2x1+1)(2x2+1) |
∵x1<x2∴2x1<2x22x2-2x1>0(11分)
∵2x1+1>0,2x2+1>0∴
| 2x2-2x1 |
| (2x1+1)(2x2+1) |
∴f(x1)-f(x2)>0,∴f(x1)>f(x2)(12分)
∴f(x)是R上的减函数(13分)
点评:本题的考点是用奇函数的定义求系数和用定义法证明函数的单调性,注意变形结果的形式和题意,
是基础题.
是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
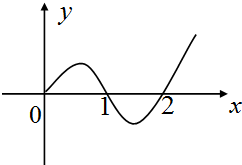 已知定义域为R的奇函数f(x)在x≥0时的图象如图所示,则不等式xf(x)<0的解集为( )
已知定义域为R的奇函数f(x)在x≥0时的图象如图所示,则不等式xf(x)<0的解集为( )