题目内容
设 a>0且a≠1),g(x)是f(x)的反函数.
a>0且a≠1),g(x)是f(x)的反函数.(Ⅰ)设关于x的方程求
 在区间[2,6]上有实数解,求t的取值范围;
在区间[2,6]上有实数解,求t的取值范围;(Ⅱ)当a=e,e为自然对数的底数)时,证明:
 ;
;(Ⅲ)当0<a≤
 时,试比较|
时,试比较| |与4的大小,并说明理由.
|与4的大小,并说明理由.
【答案】分析:(Ⅰ)求出g(x), 在[2,6]上有实数解,求出t的表达式,利用导数确定t 的范围;
在[2,6]上有实数解,求出t的表达式,利用导数确定t 的范围;
(Ⅱ)a=e求出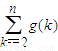 ,利用导数推出是增函数,求出最小值,即可证明
,利用导数推出是增函数,求出最小值,即可证明 ;
;
(Ⅲ)利用放缩法,求出| |的取值范围,最后推出小于4即可.
|的取值范围,最后推出小于4即可.
解答:解:(1)由题意,得ax= >0
>0
故g(x)= ,x∈(-∞,-1)∪(1,+∞)
,x∈(-∞,-1)∪(1,+∞)
由 得t=(x-1)2(7-x),x∈[2,6]
得t=(x-1)2(7-x),x∈[2,6]
则t′=-3x2+18x-15=-3(x-1)(x-5)
列表如下:
所以t最小值=5,t最大值=32
所以t的取值范围为[5,32](5分)
(Ⅱ)
=ln( )
)
=-ln
令u(z)=-lnz2- =-2lnz+z-
=-2lnz+z- ,z>0
,z>0
则u′(z)=- =(1-
=(1- )2≥0
)2≥0
所以u(z)在(0,+∞)上是增函数
又因为 >1>0,所以u(
>1>0,所以u( )>u(1)=0
)>u(1)=0
即ln >0
>0
即 (9分)
(9分)
(3)设a=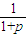 ,则p≥1,1<f(1)=
,则p≥1,1<f(1)= ≤3,
≤3,
当n=1时,|f(1)-1|= ≤2<4,
≤2<4,
当n≥2时,
设k≥2,k∈N*时,则f(k)=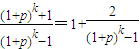 ,
,
=1+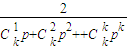
所以1<f(k)≤1+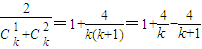 ,
,
从而n-1< ≤n-1+
≤n-1+ =n+1-
=n+1- <n+1,
<n+1,
所以n< <f(1)+n+1≤n+4,
<f(1)+n+1≤n+4,
综上所述,总有|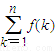 -n|<4.
-n|<4.
点评:本小题考产函数、反函数、方程、不等式、导数及其应用等基础知识,考查化归、分类整合等数学思想方法,以及推理论证、分析与解决问题的能力.
 在[2,6]上有实数解,求出t的表达式,利用导数确定t 的范围;
在[2,6]上有实数解,求出t的表达式,利用导数确定t 的范围;(Ⅱ)a=e求出
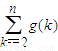 ,利用导数推出是增函数,求出最小值,即可证明
,利用导数推出是增函数,求出最小值,即可证明 ;
;(Ⅲ)利用放缩法,求出|
 |的取值范围,最后推出小于4即可.
|的取值范围,最后推出小于4即可.解答:解:(1)由题意,得ax=
 >0
>0故g(x)=
 ,x∈(-∞,-1)∪(1,+∞)
,x∈(-∞,-1)∪(1,+∞)由
 得t=(x-1)2(7-x),x∈[2,6]
得t=(x-1)2(7-x),x∈[2,6]则t′=-3x2+18x-15=-3(x-1)(x-5)
列表如下:
| x | 2 | (2,5) | 5 | (5,6) | 6 |
| t' | + | - | |||
| t | 5 | 递增 | 极大值32 | 递减 | 25 |
所以t的取值范围为[5,32](5分)
(Ⅱ)

=ln(
 )
)=-ln

令u(z)=-lnz2-
 =-2lnz+z-
=-2lnz+z- ,z>0
,z>0则u′(z)=-
 =(1-
=(1- )2≥0
)2≥0所以u(z)在(0,+∞)上是增函数
又因为
 >1>0,所以u(
>1>0,所以u( )>u(1)=0
)>u(1)=0即ln
 >0
>0即
 (9分)
(9分)(3)设a=
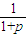 ,则p≥1,1<f(1)=
,则p≥1,1<f(1)= ≤3,
≤3,当n=1时,|f(1)-1|=
 ≤2<4,
≤2<4,当n≥2时,
设k≥2,k∈N*时,则f(k)=
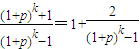 ,
,=1+
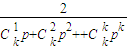
所以1<f(k)≤1+
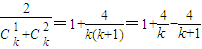 ,
,从而n-1<
 ≤n-1+
≤n-1+ =n+1-
=n+1- <n+1,
<n+1,所以n<
 <f(1)+n+1≤n+4,
<f(1)+n+1≤n+4,综上所述,总有|
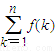 -n|<4.
-n|<4.点评:本小题考产函数、反函数、方程、不等式、导数及其应用等基础知识,考查化归、分类整合等数学思想方法,以及推理论证、分析与解决问题的能力.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目