题目内容
7.若正四棱锥的底面边长为$2\sqrt{3}cm$,体积为4cm3,则它的侧面积为8$\sqrt{3}$cm2.分析 设出正四棱锥的底面边长为a=2$\sqrt{3}$,h为高,运用体积公式求解得出h=1,求解斜高h′=2,运用面积公式求解即可.
解答 解:∵正四棱锥的底面边长为$2\sqrt{3}cm$,体积为4cm3,
∴a=2$\sqrt{3}$,h为高,
即$\frac{1}{3}×$(2$\sqrt{3}$)2×h=4,
h=1,
∴斜高为:$\sqrt{1+(\sqrt{3})^{2}}$=2,
∴侧面积为:4×$\frac{1}{2}×$2$\sqrt{3}×2$=8$\sqrt{3}$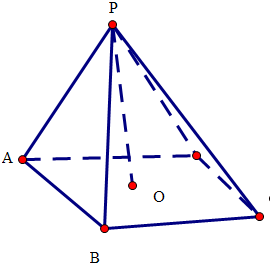
故答案为:$8\sqrt{3}$
点评 本题考查了三棱锥的几何性质,运用求解斜高,侧面积公式,属于中档题,关键是把立体问题,转化为平面问题.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 如图,已知⊙O的直径为AB,点C为⊙O上异于A,B的一点,BC⊥VA,AC⊥VB.
如图,已知⊙O的直径为AB,点C为⊙O上异于A,B的一点,BC⊥VA,AC⊥VB. 如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,PA=AB=AC=1,
如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,PA=AB=AC=1, 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点 A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是( )
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点 A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是( )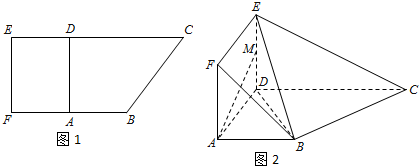
 如图,已知在长方体ABCD-A1B1C1D1中,AD=A1A=$\frac{1}{2}$AB=2,点E是棱AB上一点,且$\frac{AE}{EB}$=λ.
如图,已知在长方体ABCD-A1B1C1D1中,AD=A1A=$\frac{1}{2}$AB=2,点E是棱AB上一点,且$\frac{AE}{EB}$=λ.