Question

将长为l的棒随机折成3段，求3段长度能构成三角形的概率.

Answer 1

思路分析：本题考查与面积有关的几何概型的求法，要找清楚Ω和A.

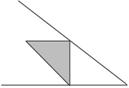
        图3-3-1

解：设A=“3段长度能构成三角形”，x、y分别表示其中两段的长度，则第3段的长度为l-x-y.

则试验的全部结果可构成集合Ω=｛(x，y)|0＜x＜l，0＜y＜l，0＜x+y＜l｝.

要使3段长度能构成三角形，当且仅当任意两段长度之和大于第3段长度,即

x+y＞l-x-yx+y＞,

x+l-x-y＞yy＜,

y+l-x-y＞xx＜.

故所求结果构成的集合A={(x,y)|x+y＞,y＜,x＜}.

由图可知，所求概率为P(A)=.

    巧解提示 一般地，若一个随机事件需要用两个连续变量(如本例中的x、y)来描述，用这两个变量的有序实数对来表示它的基本事件，利用坐标平面能顺利地建立与面积有关的几何概型.