题目内容

在△ABC中，cosA=
4
5
，cosB=
15
17
，则cosC的值是（　　）
分析：通过已知的三角形中角的范围求出 A，B的正弦值，再由两角和的余弦定理化简可得选项．
解答：解：因为 cosA=
4
5
，cosB=
15
17
，且0＜A＜π，0＜B＜π，
所以 sinA=
3
5
，sinB=
8
17
．
于是 cosC=-cos（A+B）=sinAsinB-cosAcosB=
3
5
×
8
17
-
4
5
×
15
17
=-
36
85
．
故选C．
点评：本题考查同角三角函数的基本关系，三角函数的两角和与差的余弦公式．考查计算能力．
练习册系列答案
相关题目
6、在△ABC中，cos（A-B）+sin（A+B）=2，则△ABC的形状为
等腰直角
三角形．
3、在△ABC中，cos 2B＞cos 2A是A＞B的（　　）
在△ABC中，cos(A+C)=-
3
5
，且a，c的等比中项为
35
．
（1）求△ABC的面积；
（2）若a=7，求角C．
在△ABC中，cos(A-C)+2cos2
B
2
=
5
2
，三边a，b，c成等比数列，求B．
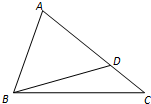精英家教网如图，在△ABC中，cos∠ABC=
1
3
，AB=6，AD=2DC，点D在AC边上．
（Ⅰ）若BC=AC，求sin∠ADB；
（Ⅱ）若BD=4
3
，求BC的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网