题目内容
已知函数 在区间
在区间 上单调,且
上单调,且 ,则方程
,则方程 =0在区间
=0在区间 上( )
上( )
| A.至少有一根 | B.至多有一实根 |
| C.没有实根 | D.必有唯一的实根 |
A
解析试题分析:因为函数 在区间
在区间 上单调,且
上单调,且 ,所以由函数的零点存在定理知在区间
,所以由函数的零点存在定理知在区间 上至少有一根.
上至少有一根.
考点:本小题主要考查函数的零点存在定理的应用.
点评:利用零点存在定理解题时,要注意零点存在定理的适用条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 解所在区间为( )
解所在区间为( )
A. | B. | C. | D. |
设函数 ,则方程
,则方程 一定存在根的区间为( )
一定存在根的区间为( )
A. | B. | C. | D. |
.函数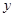 =
=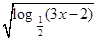 的定义域为( )
的定义域为( )
| A.[1,+∞) | B.[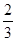 ,1] ,1] |
C.(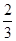 ,+∞) ,+∞) | D.(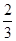 ,1] ,1] |
已知函数 在
在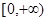 上是增函数,
上是增函数, ,若
,若 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B.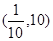 |
C. | D. |
设α∈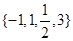 ,则使函数y=xα的定义域为R且为奇函数的所有α值为( )
,则使函数y=xα的定义域为R且为奇函数的所有α值为( )
| A.1,3 | B.-1,1 | C.-1,3 | D.-1,1,3 |
在 上,
上, 的零点有( )个
的零点有( )个
| A.0 | B.1 | C.2 | D.3 |
已知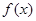 唯一的零点在区间
唯一的零点在区间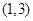 、
、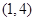 、
、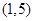 内,那么下面命题错误的
内,那么下面命题错误的
A.函数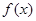 在 在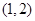 或 或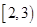 内有零点 内有零点 | B.函数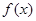 在 在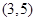 内无零点 内无零点 |
C.函数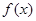 在 在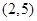 内有零点 内有零点 | D.函数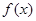 在 在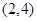 内不一定有零点 内不一定有零点 |
 ,即
,即 给出四个结论:
给出四个结论: ,②
,② ,③
,③ ,④整数
,④整数 属于同一“类”,当且仅当是
属于同一“类”,当且仅当是 ,其中正确结论的个数是( )
,其中正确结论的个数是( )