题目内容
【题目】已知椭圆![]() 的两个焦点为
的两个焦点为![]() 、
、![]() ,
,![]() 是
是![]() 与
与![]() 的等差中项,其中
的等差中项,其中![]() 、
、![]() 、
、![]() 都是正数,过点
都是正数,过点![]() 和
和![]() 的直线与原点的距离为
的直线与原点的距离为![]() .
.
(1)求椭圆的方程;
(2)点![]() 是椭圆上一动点,定点
是椭圆上一动点,定点![]() ,求△
,求△![]() 面积的最大值;
面积的最大值;
(3)已知定点![]() ,直线
,直线![]() 与椭圆交于
与椭圆交于![]() 、
、![]() 相异两点.证明:对任意的
相异两点.证明:对任意的![]() ,都存在实数
,都存在实数![]() ,使得以线段
,使得以线段![]() 为直径的圆过
为直径的圆过![]() 点.
点.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析
;(3)证明见解析
【解析】
(1)由![]() 是
是![]() 与
与![]() 的等差中项得到
的等差中项得到![]() ,设出直线的方程,利用点到直线的距离公式,列出方程,求得
,设出直线的方程,利用点到直线的距离公式,列出方程,求得![]() 的值,即可得到椭圆的方程;
的值,即可得到椭圆的方程;
(2)当椭圆上的点![]() 到直线
到直线![]() 距离最大时,△
距离最大时,△![]() 面积取得最大值,设出平行直线,即可得到结论;
面积取得最大值,设出平行直线,即可得到结论;
(3)将直线的方程代入椭圆的方程,利用韦达定理及向量知识,结合判别式,即可得到结论.
(1)由![]() 是
是![]() 与
与![]() 的等差中项,可得
的等差中项,可得![]()
过点![]() 和
和![]() 的直线方程为
的直线方程为![]() ,即
,即![]() ,
,
又由该直线与原点的距离为![]() ,由点到直线的距离公式得
,由点到直线的距离公式得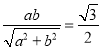
解得![]() ,所以椭圆方程为
,所以椭圆方程为![]() .
.
(2)由(1)得![]() ,直线
,直线![]() 的方程为
的方程为![]() ,且
,且![]() ,
,
当椭圆上的点![]() 到直线
到直线![]() 距离最大时,△
距离最大时,△![]() 面积取得最大值
面积取得最大值
设与直线![]() 平行的直线方程为
平行的直线方程为![]() ,
,
将其代入椭圆方程![]() ,得
,得![]() ,
,
由![]() ,解得
,解得![]() ,
,
当![]() 时,椭圆上的点
时,椭圆上的点![]() 到直线
到直线![]() 距离最大为
距离最大为![]() ,
,
此时△![]() 面积为
面积为![]() .
.
(3)将![]() 代入椭圆方程,得
代入椭圆方程,得![]() ,
,
由直线与椭圆有两个交点,所以![]() ,解得
,解得![]()
设![]() 、
、![]() ,则
,则![]() ,
,![]() ,
,
因为以![]() 为直径的圆过
为直径的圆过![]() 点,所以
点,所以![]() ,即
,即![]() ,
,
而![]() ,
,
所以![]() ,解得
,解得![]() ,
,
如果![]() 对任意的
对任意的![]() 都成立,则存在
都成立,则存在![]() ,使得以线段
,使得以线段![]() 为直径的圆过
为直径的圆过![]() 点,
点,
又因为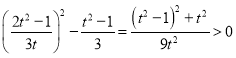 ,即
,即![]() ,
,
所以对任意的![]() ,都存在
,都存在![]() 使得以线段
使得以线段![]() 为直径的圆过
为直径的圆过![]() 点.
点.

【题目】2019年10月1日是新中国的第70个国庆日,庄重的阅兵、欢乐的游行、热烈的联欢尽显祖国的繁荣昌盛.为了了解当天某校900名高三学生的观看情况,从中抽取了100名学生,情况如下表所示:
观看情况 | 电视观看 | 网络观看 | 没有观看 |
人数 | 35 | 60 | 5 |
新时代下,网络观看使用最多的是手机,其它还有电脑、ipad等.“是否使用手机观看”与“学生的性别”之间对应的列联表如下:
使用手机观看 | 其它方式观看 | 合计 | |
男学生 | 20 | 8 | 28 |
女学生 | 20 | 12 | 32 |
合计 | 40 | 20 | 60 |
(1)估计该校高三学生当天的观看人数.
(2)当天没有观看的5名学生中,有3人第二天观看了重播.从这5名学生中任选2人求这2人第二天都看了重播的概率;
(3)根据列联表判断,能否有95%的把握认为网络观看的学生中“是否使用手机观看”与“学生的性别”有关?
附: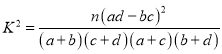 ,其中
,其中![]() .
.
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |