Question

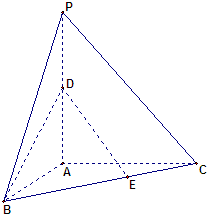在三棱锥P-ABC中，AB=AC=3，AP=4，PA⊥面ABC，∠BAC=90°，D是PA中点，点E在BC上，且BE=2CE，
（1）求证：AC⊥BD；
（2）求直线DE与PC夹角θ的余弦值；
（3）求点A到平面BDE的距离d的值．

Answer 1

分析：（1）由题意可得：所以PA⊥AC．因为∠BAC=90°，即AB⊥AC，所以AC⊥面PAB．进而得到AC⊥BD．
（2）建立空间直角坐标系，分别求出两条直线所在的向量，利用向量之间的运算计算出两个向量的夹角，进而转化为两条异面直线的夹角．
（3）设平面BDE的法向量

n

=(x，y，z)，则

n

⊥

BE

，

n

⊥

DE

，可得

n

=(2，2，3)，进而利用向量有关射影的知识可得：点A到平面BDE的距离．

解答：证明：（1）因为PA⊥面ABC，AC⊆面ABC，
所以PA⊥AC．
又因为∠BAC=90°，即AB⊥AC，
所以AC⊥面PAB．
因为BD⊆面PAB，
所以AC⊥BD．
解：以A为坐标原点建立空间直角坐标系，则由已知得：D（0，0，2），E（1，2，0），
所以

DE

=(1，2，-2)，

PC

=(0，3，-4)，

AB

=(3，0，0)，

BE

=(-2，2，0)．
（2）由上可得cos＜

DE

，

PC

＞=

DE • PC

| DE |•| PC |

=

0+6+8

1+4+4 • 0+9+16

=

14

15

＞0．
所以直线DE与PC夹角θ的余弦值为：cosθ=cos＜

DE

，

PC

＞=

14

15

．
（3）设平面BDE的法向量

n

=(x，y，z)，则

n

⊥

BE

，

n

⊥

DE

，
即：

-2x+2y+0=0 x+2y-2z=0

，
令x=2，则可得

n

=(2，2，3)．
故点A到平面BDE的距离d的值为：d=

| AB • n |

| n |

=

|6+0+0|

4+4+9

=

6 17

17

．

点评：解决此类问题的关键是熟练掌握几何体的结构特征，熟悉线面之间的关系并且利于建立空间直角坐标系，再利用空间向量的知识解决空间角与空间距离等问题．