题目内容
已知函数 的定义域为M,g(x)=ex-2的值域为N,则M∩N=( )
的定义域为M,g(x)=ex-2的值域为N,则M∩N=( )A.[2,+∞)
B.(-∞,2)
C.(-2,2)
D.∅
【答案】分析:根据分式的分母不为零,且二次根号的被开方数必须大于或等于零,解不等式得到函数f(x)的定义域M=(-∞,2),再根据指数函数y=ex的值域,得到g(x)的值域为N=(-2,+∞),最后利用交集的定义可以算出集合M∩N.
解答:解:∵分式的分母不为零,且二次根号的被开方数必须大于或等于零,
∴函数 的定义域为M,满足:
的定义域为M,满足: ,
,
解之得,M=(-∞,2),
∵指数函数y=ex的值域为(0,+∞),
∴g(x)=ex-2的值域为(-2,+∞),即N=(-2,+∞),
再计算交集,得M∩N=(-∞,2)∩(-2,+∞)=(-2,2).
故选C
点评:本题给出两个已知函数,通过求它们的定义域和值域,考查了函数的定义域求法、指数函数的值域和交集运算等知识点,属于基础题.
解答:解:∵分式的分母不为零,且二次根号的被开方数必须大于或等于零,
∴函数
 的定义域为M,满足:
的定义域为M,满足: ,
,解之得,M=(-∞,2),
∵指数函数y=ex的值域为(0,+∞),
∴g(x)=ex-2的值域为(-2,+∞),即N=(-2,+∞),
再计算交集,得M∩N=(-∞,2)∩(-2,+∞)=(-2,2).
故选C
点评:本题给出两个已知函数,通过求它们的定义域和值域,考查了函数的定义域求法、指数函数的值域和交集运算等知识点,属于基础题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 的定义域为M.
的定义域为M. 的定义域为M.
的定义域为M. 的定义域为M,函数
的定义域为M,函数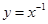 的定义域为N,则
的定义域为N,则 ( )
( ) 且
且 B.
B.  且
且 D.
D.

 的定义域为M,函数
的定义域为M,函数 的定义域为N,则
的定义域为N,则 的定义域为M,g(x)=
的定义域为M,g(x)= 的定义域为N,则M∩N=
的定义域为N,则M∩N= (B)
(B) (C)
(C) (D)
(D)