题目内容
判断下列函数的奇偶性:(1)f(x)=![]() ;
;
(2)f(x)=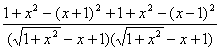 ;
;
(3)f(x)=![]() ;
;
(4)f(x)=2x3+![]() .
.
思路分析:先求函数定义域,然后用函数的奇偶性定义或其变形来判断.
解:(1)∵x2-4≥0,且4-x2≥0,∴x=±2,即f(x)的定义域是{-2,2}.
∵f(2)=0,f(-2)=0,∴f(2)=f(-2),f(2)=-f(2).
∴f(-x)=-f(x),且f(-x)=f(x).
∴f(x)既是奇函数也是偶函数.
(2)定义域是R.
f(-x)+f(x)=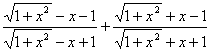
=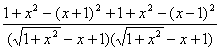
=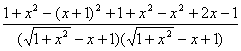 =0.
=0.
∴f(-x)=-f(x).∴f(x)是奇函数.
(3)f(x)=![]() ,定义域是(-∞,0)∪(0,+∞),
,定义域是(-∞,0)∪(0,+∞),
f(-x)=![]() =f(x),
=f(x),
∴f(x)=![]() 是偶函数.
是偶函数.
(4)f(x)=2x3+![]() ,定义域是R,
,定义域是R,
f(-x)=2(-x)3+![]() =-(2x3+
=-(2x3+![]() )=-f(x).
)=-f(x).
∴f(x)=2x3+![]() 是奇函数.
是奇函数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目