题目内容
已知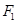 、
、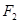 分别是椭圆C:
分别是椭圆C: 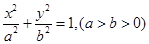 的左焦点和右焦点,O是坐标系原点, 且椭圆C的焦距为6, 过
的左焦点和右焦点,O是坐标系原点, 且椭圆C的焦距为6, 过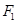 的弦AB两端点A、B与
的弦AB两端点A、B与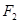 所成
所成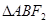 的周长是
的周长是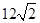 .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ) 已知点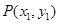 ,
,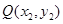 是椭圆C上不同的两点,线段
是椭圆C上不同的两点,线段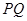 的中点为
的中点为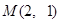 ,
,
求直线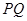 的方程
的方程
(Ⅰ)
解:设椭圆C:  的焦距为2c,
的焦距为2c,
∵椭圆C:  的焦距为2, ∴2c=6,即c=3…………1分
的焦距为2, ∴2c=6,即c=3…………1分
又∵ 、
、 分别是椭圆C:
分别是椭圆C:  的左焦点和右焦点,且过
的左焦点和右焦点,且过 的弦AB两端点A、B与
的弦AB两端点A、B与 所成⊿AB
所成⊿AB 的周长是
的周长是 .
.
∴⊿AB 的周长 = AB+(AF2+BF2)= (AF1+BF1)+
(AF2+BF2)=4
的周长 = AB+(AF2+BF2)= (AF1+BF1)+
(AF2+BF2)=4 =
=
∴ …………4分
…………4分
又∵ , ∴
, ∴ ∴椭圆C的方程是
∴椭圆C的方程是 …………6分
…………6分
(Ⅱ)解一:  点
点 ,
, 是椭圆C上不同的两点,
是椭圆C上不同的两点,
∴ ,
, .…………7分
.…………7分
以上两式相减得: ,…………8分
,…………8分
即 ,
, ,…9分
,…9分
∵线段 的中点为
的中点为 ,∴
,∴ . …10分
. …10分
∴ ,…………11分
,…………11分
当 ,由上式知,
,由上式知, 则
则 重合,与已知矛盾,因此
重合,与已知矛盾,因此 ,………12分
,………12分
∴ .
……………………13分
.
……………………13分
∴直线 的方程为
的方程为 ,即
,即 . ………14分
. ………14分
解二:
当直线 的不存在时,
的不存在时,  的中点在
的中点在 轴上, 不符合题意.
轴上, 不符合题意.
故可设直线 的方程为
的方程为 ,
,  . ……8分
. ……8分
由 消去
消去 ,得
,得 (*)
(*)
 .
………10分
.
………10分

 的中点为
的中点为 ,
,
 .
. .解得
.解得 . ………12分
. ………12分
此时方程(*)为 ,其判别式
,其判别式 .………13分
.………13分
∴直线 的方程为
的方程为 .
………14分
.
………14分
【解析】略

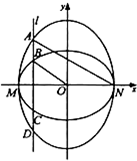 如图,已知MN分别是椭圆C1、C2的长轴和短轴,且C1、C2的离心率都等于
如图,已知MN分别是椭圆C1、C2的长轴和短轴,且C1、C2的离心率都等于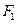 、
、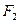 分别是椭圆C:
分别是椭圆C: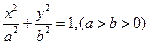 的左焦点和右焦点,O是坐标系原点, 且椭圆C的焦距为6, 过
的左焦点和右焦点,O是坐标系原点, 且椭圆C的焦距为6, 过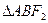 的周长是
的周长是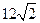 .
.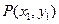 ,
,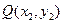 是椭圆C上不同的两点,线段
是椭圆C上不同的两点,线段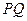 的中点为
的中点为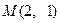 ,
,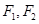 分别是椭圆
分别是椭圆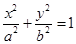 的左、右焦点,过
的左、右焦点,过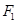 且垂直于
且垂直于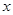 轴的直线与椭圆交于A、B两点,若
轴的直线与椭圆交于A、B两点,若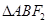 为正三角形,则该椭圆的离心率
为正三角形,则该椭圆的离心率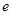 是(
)
是(
)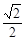 B.
B.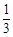 C.
C.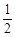 D.
D.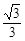
 、
、 分别是椭圆C:
分别是椭圆C:  的左焦点和右焦点,O是坐标系原点, 且椭圆C的焦距为6, 过
的左焦点和右焦点,O是坐标系原点, 且椭圆C的焦距为6, 过 两端点
两端点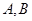 与
与 的周长是
的周长是 .
. ,
, 是椭圆C上不同的两点,线段
是椭圆C上不同的两点,线段 的中点为
的中点为 .
. 、
、 ,试问四点
,试问四点 、
、 、
、