Question

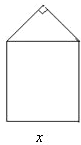如图，某单位用木料制作如图所示的框架，框架的下部是边长分别为x，y（单位：米）的矩形，上部是斜边长为x的等腰直角三角形，要求框架围成的总面积为8平方米．
（Ⅰ）求x，y的关系式，并求x的取值范围；
（Ⅱ）问x，y分别为多少时用料最省？

Answer 1

分析：（I）根据三角形和矩形面积公式得出x和y的关系式，确保有意义求出x的范围得到定义域；
（II）根据解析式进而表示出框架用料长度为根据均值不等式求得l的最小值，求得此时的x和y．

解答：解：（Ⅰ）由题意得：x•y+

1

2

x•

x

2

=8(x＞0，y＞0)，
∴y=

8

x

-

x

4

，
∵y=

8

x

-

x

4

＞0
∴0＜x＜4

2

（6分）
（Ⅱ）设框架用料长度为l，则l=2x+2y+

2

x(9分)
=(

3

2

+

2

)x+

16

x

≥4

6+4 2

(=8+4

2

)(12分)
当且仅当(

3

2

+

2

)x=

16

x

，x=8-4

2

，y=2

2

，满足0＜x＜4

2

(15分)
答：故当x为2.343m，y为2.828m时，用料最省．

点评：本题主要考查了基本不等式在最值问题中的应用．注意取得最值时的条件是否成立，属于基础题．