题目内容
经市场调查，某旅游城市在过去的一个月内(以30天计)，旅游人数f(t)(万人)与时间t(天)的函数关系近似满足f(t)＝4＋
，人均消费g(t)(元)与时间t(天)的函数关系近似满足g(t)＝115－|t－15|.
(1)求该城市的旅游日收益w(t)(万元)与时间t(1≤t≤30，t∈N*)的函数关系式；
(2)求该城市旅游日收益的最小值(万元)．
，人均消费g(t)(元)与时间t(天)的函数关系近似满足g(t)＝115－|t－15|.(1)求该城市的旅游日收益w(t)(万元)与时间t(1≤t≤30，t∈N*)的函数关系式；
(2)求该城市旅游日收益的最小值(万元)．
（1）
(115－|t－15|)(1≤t≤30，t∈N*)（2）403
万元
(115－|t－15|)(1≤t≤30，t∈N*)（2）403万元(1)由题意得，w(t)＝f(t)·g(t)＝(115－|t－15|)(1≤t≤30，t∈N*)．(5分)
(2)因为w(t)＝
(7分)，
①当1≤t＜15时，w(t)＝(t＋100)＝4
＋401≥4×2
＋401＝441，
当且仅当t＝
，即t＝5时取等号．(10分)
②当15≤t≤30时，w(t)＝(130－t)＝519＋
，
可证w(t)在t∈[15,30]上单调递减，所以当t＝30时，w(t)取最小值为403.(13分)
由于403＜441，所以该城市旅游日收益的最小值为403万元．(14分)
(115－|t－15|)(1≤t≤30，t∈N*)．(5分)(2)因为w(t)＝
(7分)，①当1≤t＜15时，w(t)＝
(t＋100)＝4＋401≥4×2＋401＝441，当且仅当t＝
，即t＝5时取等号．(10分)②当15≤t≤30时，w(t)＝
(130－t)＝519＋，可证w(t)在t∈[15,30]上单调递减，所以当t＝30时，w(t)取最小值为403
.(13分)由于403
＜441，所以该城市旅游日收益的最小值为403万元．(14分)
练习册系列答案
阅读快车系列答案
相关题目
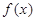是定义在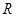
上的奇函数，当
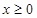时，
．
；
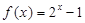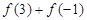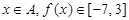，求区间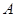
．
若|f(x)|≥ax，则a的取值范围是________．
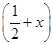＝f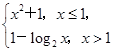
则满足f(x)≤2的x的取值范围是( )．
，
，则下列选项正确的是（ ）
