Question

已知数列{a_n}满足2a_n+1=a_n+a_n+2（n∈N^*），它的前n项和为S_n，且a₃=5，S₆=36．

（1）求数列{a_n}的通项公式；

（2）设b_n=6ⁿ+（﹣1）^n﹣1λ•2a_n（λ为正整数，n∈N^*），试确定λ的值，使得对任意n∈N^*，都有b_n+1＞b_n成立．

Answer 1

考点：

数列递推式；数列的函数特性．

专题：

等差数列与等比数列．

分析：

（1）利用等差数列的定义和通项公式、前n项和公式即可得出；

（2）利用（1）的结论，通过作差b_n+1﹣b_n并对n分奇偶讨论即可得出．

解答：

解：（1）∵对于∀n∈N^*，都有2a_n+1=a_n+a_n+2，∴数列{a_n}是等差数列，设公差为d，

∵a₃=5，S₆=36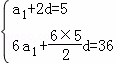，∴，解得．

∴a_n=1+（n﹣1）×2=2n﹣1．（n∈N^*）．

（2）由（1）可得：，（λ为正整数，n∈N^*），

∴b_n+1﹣b_n=6ⁿ⁺¹+（﹣1）ⁿλ•2（2n+1）﹣[6ⁿ+（﹣1）^n﹣1λ•2（2n﹣1）]

=5×6ⁿ+（﹣1）ⁿλ×4，

当n为偶数时，∵λ为正整数，∴b_n+1﹣b_n＞0成立；

当n奇数时，要使5×6ⁿ﹣4λ＞0恒成立，则，

∵关于n单调递增，∴当n=1时，取得最小值，又λ为正整数，取λ=7，6，5，4，3，2，1．

∴当λ=7，6，5，4，3，2，1时，使得对任意n∈N^*，都有b_n+1＞b_n成立．

点评：

熟练掌握等差数列的定义和通项公式、前n项和公式、作差法、分类讨论的思想方法是解题的关键．