题目内容
如图所示,已知正方体ABCD-A1B1C1D1中,点E为棱CC1上的动点.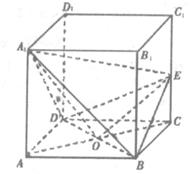
(Ⅰ)求证:A1E⊥BD;
(Ⅱ)当点E恰为棱CC1的中点时,求证:平面A1BD⊥平面EBD;
(Ⅲ)在棱CC1上是否存在一个点E,使二面角A1-BD-E的大小为45°?如果存在,试确定点E在棱CC1上的位置;如果不存在,请说明理由.
法一:(Ⅰ)证明:连结AC,则BD⊥AC

又∵EC⊥平面ABCD,AA1⊥平面ABCD,
∴AC是A1E在平面ABCD上的射影,
由三垂线定理知:A1E⊥BD
(Ⅱ)设AC∩BD=0,连结A1O、EO
∵A1D=A1B,∴A1O⊥BD,同理可证EO⊥BD,
∴∠A1OE是二面角A1-BD-E的平面角.
设正方体的棱长为2a,由平面几何知识,得
A1O=![]() a,EO=
a,EO=![]() a,A1E=3a,
a,A1E=3a,
∴A1E2=A1O2+EO2,∴∠A1OE=![]() ,即:
,即:
平面A1ED⊥平面EBD
(Ⅲ)在正方体ABCD-A1B1C1D1中,假设棱CC1上存在点E,使二面角A1-BD-E的大小为![]() ,由(Ⅱ)知∠A1OE=
,由(Ⅱ)知∠A1OE=![]()
设正方体ABCD-A1B1C1D1的棱长为2a,EC=x,
由平面几何知识,得:EO=![]() ,
,
A1O=![]() a,A1E=
a,A1E=![]()
∴在ΔA1OE中,由余弦定理得:
A1E2=A1O2+EO2-2 A1O·EO·cos∠A1OE
即:x2-8ax-2a2=0,(x>a),解得:x=(4±3![]() )a
)a
∵(4+3![]() )a>2a,(4-3
)a>2a,(4-3![]() )a<0,
)a<0,
∴棱CC1上不存在满足条件的点E
法二:以DA、DC、DD1所在直线为x轴、y轴、z轴建立空间直角坐标系
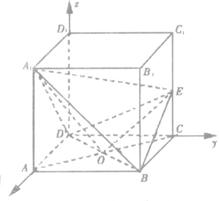
(Ⅰ)设正方体的棱长为a,则:A(a,0,0),B(a,a,0),C(0,a,0),A1(a,0,a),C1(0,a,a),D(0,0,0)设E(0,a,x),则![]() =(-a,a,x-a),
=(-a,a,x-a), ![]() =(-a,-a,0)
=(-a,-a,0)
∵![]() =(-a)·(-a)+a·(-a)+(x-a)·0=0,
=(-a)·(-a)+a·(-a)+(x-a)·0=0,
∴![]() ,即A1E⊥BD
,即A1E⊥BD
(Ⅱ)由题设可知E(0,a,![]() ),设BD的中点为O,则O(
),设BD的中点为O,则O(![]() ,
,![]() ,0).
,0).
∴![]() =(-
=(-![]() ,
,![]() ,
,![]() ),
),![]() =(-a,-a,0)
=(-a,-a,0)
则![]() ·
·![]() =(-
=(-![]() )·(-a)+
)·(-a)+![]() ·(-a)+
·(-a)+![]() ·0=0,
·0=0,
∴![]() ⊥
⊥![]() , 同理可证
, 同理可证![]() ⊥
⊥![]() ,
,
∴∠A1OE是二面角A1-BD-E的平面角
又![]() =(
=(![]() ,-
,-![]() ,a),故:
,a),故:
![]() ·
·![]() =
=![]() ·(-
·(-![]() )+(-
)+(-![]() )·
)·![]() +a·
+a·![]() =0
=0
∴![]() ·
·![]() =0,则∠A1OE=
=0,则∠A1OE=![]() ,
,
∴平面A1BD⊥平面EBD
(Ⅲ)假设满足题意的点E存在,设E(0,a,x),(0≤x≤a),
则![]() =(-
=(-![]() ,
,![]() ,x),
,x),![]() =(
=(![]() ,-
,-![]() ,a).
,a).
∴cos∠A1OE=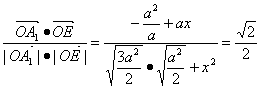 ,
,
解得:x=![]()
由x=![]() >a,x=
>a,x=![]() <0,与0≤x≤a矛盾,
<0,与0≤x≤a矛盾,
故棱CC1上不存在满足条件的点E

 名校课堂系列答案
名校课堂系列答案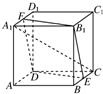 如图所示,已知正方体ABCD-A1B1C1D1的棱长为a,E,F分别是BC,A1D1的中点.
如图所示,已知正方体ABCD-A1B1C1D1的棱长为a,E,F分别是BC,A1D1的中点.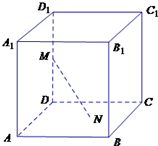 如图所示,已知正方体ABCD-A1B1C1D1的棱长为2,长为2的线段MN的一个端点M在棱DD1上运动,另一端点N在正方形ABCD内运动,则MN的中点的轨迹的面积为( )
如图所示,已知正方体ABCD-A1B1C1D1的棱长为2,长为2的线段MN的一个端点M在棱DD1上运动,另一端点N在正方形ABCD内运动,则MN的中点的轨迹的面积为( )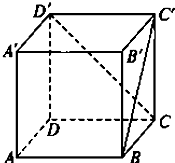 如图所示,已知正方体ABCD-A′B′C′D′,求:
如图所示,已知正方体ABCD-A′B′C′D′,求:
 的概率P1;
的概率P1; 的概率P2。
的概率P2。