题目内容
17.已知数列{an},满足a1=$\frac{1}{3}$,an+1=an•3n(n∈N*),则数列{an}的通项公式为( )| A. | an=3${\;}^{\frac{{a}^{2}-2n}{2}}$ | B. | an=3${\;}^{\frac{{n}^{2}-2n-2}{2}}$ | C. | an=3${\;}^{\frac{{n}^{2}-n-2}{2}}$ | D. | an=3${\;}^{\frac{{2}_{n}-{n}^{2}}{2}}$ |
分析 通过对an+1=an•3n两边同时取对数可知log3an+1=log3an+n,利用累加法计算即得结论.
解答 解:∵an+1=an•3n(n∈N*),
∴log3an+1=log3(an•3n)=log3an+n,
∴log3an=log3an-1+n-1,
log3an-1=log3an-2+n-2,
…
log3a2=log3a1+1,
累加得:log3an=log3a1+1+2+…+(n-1)
=$lo{g}_{3}\frac{1}{3}$+$\frac{n(n-1)}{2}$
=-1+$\frac{n(n-1)}{2}$
=$\frac{{n}^{2}-n-2}{2}$,
∴an=${3}^{\frac{{n}^{2}-n-2}{2}}$,
故选:C.
点评 本题考查数列的通项,注意解题方法的积累,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.若x,y>0且x+y>2,则$\frac{1+y}{x}$和$\frac{1+x}{y}$的值满足( )
| A. | $\frac{1+y}{x}$和$\frac{1+x}{y}$中至少有一个小于2 | B. | $\frac{1+y}{x}$和$\frac{1+x}{y}$都等于2 | ||
| C. | $\frac{1+y}{x}$和$\frac{1+x}{y}$都大于2 | D. | 不确定 |
9.点P坐标为(sinα-cosα,sinα+cosα),当α∈(0,2π)时,P在第二象限,则α取值范围为( )
| A. | (-$\frac{π}{4}$,$\frac{π}{4}$) | B. | (0,$\frac{π}{4}$)∪($\frac{7π}{4}$,2π) | C. | (0,$\frac{π}{4}$)∪($\frac{5π}{4}$,$\frac{7π}{4}$) | D. | ($\frac{π}{4}$,$\frac{3π}{4}$) |
6.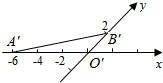 如图,△O′A′B′是水平放置的△OAB的直观图,则△OAB的面积是( )
如图,△O′A′B′是水平放置的△OAB的直观图,则△OAB的面积是( )
 如图,△O′A′B′是水平放置的△OAB的直观图,则△OAB的面积是( )
如图,△O′A′B′是水平放置的△OAB的直观图,则△OAB的面积是( )| A. | 6 | B. | 3$\sqrt{2}$ | C. | 6$\sqrt{2}$ | D. | 12 |