Question

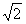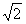如图，四棱锥P-ABCD的底面是AB=2，BC=的矩形，侧面PAB是等边三角形，且侧面PAB⊥底面ABCD。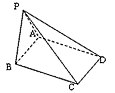

（Ⅰ）证明：BC⊥侧面PAB；
（Ⅱ）证明：侧面PAD⊥侧面PAB；
（Ⅲ）求侧棱PC与底面ABCD所成角的大小。

Answer 1

（Ⅰ）证明：∵侧面PAB垂直于底面ABCD，且侧面PAB与底面ABCD的交线是AB，
在矩形ABCD中，BC⊥AB，
∴BC⊥侧面PAB。
（Ⅱ）证明：在矩形ABCD中，AD∥BC，BC⊥侧面PAB，
∴AD⊥侧面PAB，
又AD在平面PAD上，
所以，侧面PAD⊥侧面PAB。
（Ⅲ）解：在侧面PAB内，过点P做PE⊥AB.垂足为E，连结EC，
∵侧面PAB与底面ABCD 的交线是AB，PE⊥AB，
∴PE⊥底面ABCD，
于是EC为PC在底面ABCD内的射影，
∴∠PCE为侧棱PC与底面ABCD所成的角，
在△PAB和△BEC中，易求得PE=，EC=，
∴在Rt△PEC中，∠PCE=45°。