题目内容
函数 的图象
的图象
- A.关于原点对称
- B.关于y轴对称
- C.关于点
 对称
对称 - D.关于直线
 对称
对称
D
分析:观察已知可知符合两角和的正弦,故可得f(x)=sin(2x- ),针对每个命题进行判断,排除错误选项即可.
),针对每个命题进行判断,排除错误选项即可.
解答:∵ =
= =sin(2x
=sin(2x );
);
A,由于函数为非奇非偶函数,故 A错误
B:根据A可判断B错误
C:根据对称中心是函数与轴的交点,代入检验可得f(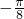 )=-1可知C错误
)=-1可知C错误
D:根据对称轴处取得函数的最值,代入检验可得 可知D正确
可知D正确
故选D.
点评:本题主要考查了利用两角和的正弦公式对函数化简,进一步考查三角函数的性质,三角函数的位置特征要准确掌握,如对称中心是函数与x轴的交点,对称轴经过图象的最高点或最低点,奇函数的图象关于原点对称,偶函数的图象关于 y轴对称.
分析:观察已知可知符合两角和的正弦,故可得f(x)=sin(2x-
 ),针对每个命题进行判断,排除错误选项即可.
),针对每个命题进行判断,排除错误选项即可.解答:∵
 =
= =sin(2x
=sin(2x );
);A,由于函数为非奇非偶函数,故 A错误
B:根据A可判断B错误
C:根据对称中心是函数与轴的交点,代入检验可得f(
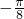 )=-1可知C错误
)=-1可知C错误D:根据对称轴处取得函数的最值,代入检验可得
 可知D正确
可知D正确故选D.
点评:本题主要考查了利用两角和的正弦公式对函数化简,进一步考查三角函数的性质,三角函数的位置特征要准确掌握,如对称中心是函数与x轴的交点,对称轴经过图象的最高点或最低点,奇函数的图象关于原点对称,偶函数的图象关于 y轴对称.

练习册系列答案
相关题目