题目内容
设ABCDEF为正六边形,一只青蛙开始在顶点A处,它每次可随意地跳到相邻两顶点之一.若在5次之内跳到D点,则停止跳动;若5次之内不能到达D点,则跳完5次也停止跳动,那么这只青蛙从开始到停止,可能出现的不同跳法共 种.
【答案】分析:由题意,青蛙不能经过跳1次、2次或4次到达D点,故可以分青蛙跳3次到达D点和青蛙一共跳5次后停止两种情况分别计算,利用分类计数原理可得结论.
解答:解:青蛙不能经过跳1次、2次或4次到达D点.故青蛙的跳法只有下列两种:
(1)青蛙跳3次到达D点,有ABCD,AFED两种跳法;
(2)青蛙一共跳5次后停止,那么,前3次的跳法一定不到达D,只能到达B或F,
则共有AFEF,AFAF,ABAF,ABCB,ABAB,AFAB这6种跳法.随后的两次跳法各有四种,
比如由F出发的有:FEF,FED,FAF,FAB共四种.因此这5次跳法共有6×4=24种不同跳法.
所以,一共有2+24=26种不同跳法.
故答案为:26.
点评:本题考查加法原理和乘法原理的运用,考查了学生分析解答问题的能力.解题的关键是从已知分析得到,青蛙不能经过跳1次、2次或4次到达D点,从而从青蛙跳3次到达D点和青蛙一共跳5次后停止两种情况入手分别计算.
解答:解:青蛙不能经过跳1次、2次或4次到达D点.故青蛙的跳法只有下列两种:
(1)青蛙跳3次到达D点,有ABCD,AFED两种跳法;
(2)青蛙一共跳5次后停止,那么,前3次的跳法一定不到达D,只能到达B或F,
则共有AFEF,AFAF,ABAF,ABCB,ABAB,AFAB这6种跳法.随后的两次跳法各有四种,
比如由F出发的有:FEF,FED,FAF,FAB共四种.因此这5次跳法共有6×4=24种不同跳法.
所以,一共有2+24=26种不同跳法.
故答案为:26.
点评:本题考查加法原理和乘法原理的运用,考查了学生分析解答问题的能力.解题的关键是从已知分析得到,青蛙不能经过跳1次、2次或4次到达D点,从而从青蛙跳3次到达D点和青蛙一共跳5次后停止两种情况入手分别计算.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目




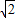 ,M是PA的中点.
,M是PA的中点.