题目内容
已知f(x)是定义在R上的函数,且满足f(x)+f(x-1)=1,当x∈[0,1]时,f(x)=①f(x)是周期函数,且周期为2; ②当x∈[1,2]时,f(x)=2x-
其中正确命题的个数是( )
A.1 B.2 C.3 D.4
解析:从认知f(x)的性质入手,由f(x)+f(x-1)=1得f(x-1)=1-f(x) (※) ∴f(x-2)=1-f(x-1) (※※)
∴由(※),(※※)得f(x)=f(x-2) ∴f(x)为周期函数,且2是f(x)的一个周期. (1)由上述推理可知 ① 正确.
(2)当x∈[1,2]时,有x-1∈[0,1].∴由题设得f(x)=1-f(x-1)=1-(x-1) =2x-x
=2x-x , 由此可知 ② 正确
, 由此可知 ② 正确
(3)由已知条件以及结果 ① ② 得 ,又f(
,又f( )=
)= , ∴f(
, ∴f( )≠f(-
)≠f(- )
)
∴f(x)不是偶函数即③不正确;
(4)由已知条件与f(x)的周期性得f(-2005.5)=f(-2005.5+2×1003)= f( )=
)= 故④不正确.
故④不正确.
于是由(1)(2)(3)(4)知,本题应选B.
∴由(※),(※※)得f(x)=f(x-2) ∴f(x)为周期函数,且2是f(x)的一个周期. (1)由上述推理可知 ① 正确.
(2)当x∈[1,2]时,有x-1∈[0,1].∴由题设得f(x)=1-f(x-1)=1-(x-1)
(3)由已知条件以及结果 ① ② 得
∴f(x)不是偶函数即③不正确;
(4)由已知条件与f(x)的周期性得f(-2005.5)=f(-2005.5+2×1003)= f(
于是由(1)(2)(3)(4)知,本题应选B.

练习册系列答案
相关题目
 ) =
f(x)-f(y)
) =
f(x)-f(y) 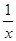 ) <2
) <2  ∪
∪ 上的奇函数,当
上的奇函数,当 时,f (x)的图象如图所示,那么f (x)的值域是
时,f (x)的图象如图所示,那么f (x)的值域是
