题目内容
关于x的不等式(1+m)x2+mx+m<x2+1对x∈R恒成立,则实数m的取值范围是( )
| A.(-∞,0) | B.(-∞,0)∪ |
| C.(-∞,0] | D.(-∞,0]∪ |
C
解:因为当m=-1时,显然成立,
当 时,要使不等式对一切实数恒成立,则需满足开口向下,判别式小于零
时,要使不等式对一切实数恒成立,则需满足开口向下,判别式小于零
即mx2+mx+m-1<0, ,选C
,选C
当
 时,要使不等式对一切实数恒成立,则需满足开口向下,判别式小于零
时,要使不等式对一切实数恒成立,则需满足开口向下,判别式小于零即mx2+mx+m-1<0,
 ,选C
,选C
练习册系列答案
相关题目
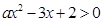 的解集为
的解集为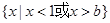
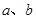 ;
;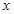 的不等式
的不等式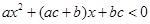 .
.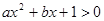 的解集为
的解集为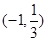 ,则
,则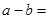 .
. 的不等式:
的不等式: 
 ,解关于
,解关于 的不等式
的不等式 .
. 的不等式
的不等式 ,在
,在 上恒成立,则实数
上恒成立,则实数 的范围为( )
的范围为( )



 的解集是 ( )
的解集是 ( ) ,集合
,集合 ,
, ,则
,则 等于
等于



 的不等式:
的不等式: