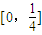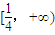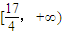题目内容
若函数y=x2-
x+
的图象在点M(0，
)处的切线l与圆C：x2+y2=1相交，则点P（m，n）与圆C的位置关系是（ ）
| m |
| n |
| 1 |
| n |
| 1 |
| n |
| A、圆内 | B、圆外 |
| C、圆上 | D、圆内或圆外 |
分析：根据f′（0）求出切线的斜率，表示出切线方程，因为切线l与圆相交得到圆心到直线的距离小于半径列出关系式，得到根据点到圆心的距离与半径比较大小得到点与圆C的位置关系．
解答：解：函数f（x）图象在M处切线l的斜率k=f′（0）=-
，
∴切线l的方程为mx+ny=1，
∵与x2+y2=1相交，所以圆心（0，0）到切线l的距离d=
=
＜1解得
＞ 1，
而P（m，n）到圆心（0，0）的距离
＞ 1，所以点在圆外．
故选B
| m |
| n |
∴切线l的方程为mx+ny=1，
∵与x2+y2=1相交，所以圆心（0，0）到切线l的距离d=
| |1| | ||
|
| 1 | ||
|
| m2+n2 |
而P（m，n）到圆心（0，0）的距离
| m2+n2 |
故选B
点评：本题是一道综合题，要求学生会根据d与r的大小判断点与圆的位置关系，理解直线与圆垂直时圆心到直线的距离等于半径，以及灵活运用点到直线的距离公式化简求值．会根据导函数求曲线上某点切线的斜率．
练习册系列答案
考前必练系列答案
相关题目
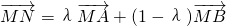的点N，得
．对于实数k，如果不等式|MN|≤k对λ∈[0，1]恒成立，那么就称函数f（x）在[a，b]上“k阶线性近似”．若函数y=x2+x在[1，2]上“k阶线性近似”，则实数k的取值范围为
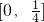
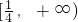
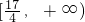
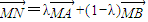的点N，得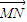
．对于实数k，如果不等式|MN|≤k对λ∈[0，1]恒成立，那么就称函数f（x）在[a，b]上“k阶线性近似”．若函数y=x2+x在[1，2]上“k阶线性近似”，则实数k的取值范围为（ ）
